题目内容
下列说法正确的是( )
| A、曲线的切线和曲线的交点有且只有一个 |
| B、过曲线上的一点作曲线的切线,这点一定是切点 |
| C、若f′(x0)不存在,则曲线y=f(x)在点(x0,f(x0))处无切线 |
| D、若y=f(x)在点(x0,f(x0))处有切线,则f′(x0)不一定存在 |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:举例说明选项A,B错误;由可导与连续的关系说明C错误,D正确.
解答:
解:对于A,曲线的切线和曲线的交点不一定唯一,如曲线y=x3+1在(-
,
)处的切线与曲线有另外一个交点(1,2);
对于B,过曲线上的一点作曲线的切线,这点不一定是切点,如经过曲线上一点但是不是在该点与曲线相切而是在其他地方相切,比如y=y=x3与y=3x-2相切于点(1,1),同时经过点另外一点(a,b),我们就可以说过点(a,b)的直线y=3x-2与曲线y=x3相切,但切点是(1,1)而不是(a,b);
对于C,若f′(x0)不存在,则曲线y=f(x)在点(x0,f(x0))处无切线错误,如曲线在某点处的切线垂直于x轴,此时f′(x0)不存在,但曲线y=f(x)在点(x0,f(x0))处有切线;
对于D,由曲线在一点有平行y轴的切线,且函数在该点不连续,则f′(x0)不一定存在.
故选:D.
| 1 |
| 2 |
| 7 |
| 8 |
对于B,过曲线上的一点作曲线的切线,这点不一定是切点,如经过曲线上一点但是不是在该点与曲线相切而是在其他地方相切,比如y=y=x3与y=3x-2相切于点(1,1),同时经过点另外一点(a,b),我们就可以说过点(a,b)的直线y=3x-2与曲线y=x3相切,但切点是(1,1)而不是(a,b);
对于C,若f′(x0)不存在,则曲线y=f(x)在点(x0,f(x0))处无切线错误,如曲线在某点处的切线垂直于x轴,此时f′(x0)不存在,但曲线y=f(x)在点(x0,f(x0))处有切线;
对于D,由曲线在一点有平行y轴的切线,且函数在该点不连续,则f′(x0)不一定存在.
故选:D.
点评:本题考查了利用导数研究过曲线上某点处的切线方程,考查了可导与连续间的关系,关键在于学生对导数概念的理解,是中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
以椭圆
+
=1的左焦点为焦点,以坐标原点为顶点的抛物线方程为( )
| x2 |
| 4 |
| y2 |
| 3 |
| A、y2=-4x |
| B、y2=-2x |
| C、y2=-8x |
| D、y=-x |
 如图是正四面体的平面展开图,M、N、G分别为DE、BE、FE的中点,则在这个正四面体中,MN与CG所成角的大小为
如图是正四面体的平面展开图,M、N、G分别为DE、BE、FE的中点,则在这个正四面体中,MN与CG所成角的大小为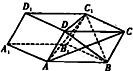 已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2
已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2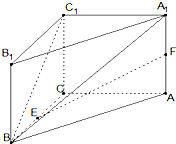 在直三棱柱ABC-A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BC A1A的中点.
在直三棱柱ABC-A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BC A1A的中点.