题目内容
设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f′(x),且有2f(x)+xf′(x)>x2,则不等式(x+2014)2f(x+2014)-4f(-2)>0的解集为( )
| A、(-∞,-2012) |
| B、(-2012,0) |
| C、(-∞,-2016) |
| D、(-2016,0) |
考点:导数的运算
专题:导数的综合应用
分析:根据条件,构造函数,利用函数的单调性和导数之间的关系,将不等式进行转化即可得到结论.
解答:
解:由2f(x)+xf′(x)>x2,(x<0),
得:2xf(x)+x2f′(x)<x3,
即[x2f(x)]′<x3<0,
令F(x)=x2f(x),
则当x<0时,
得F′(x)<0,即F(x)在(-∞,0)上是减函数,
∴F(x+2014)=(x+2014)2f(x+2014),F(-2)=4f(-2),
即不等式等价为F(x+2014)-F(-2)>0,
∵F(x)在(-∞,0)是减函数,
∴由F(x+2014)>F(-2)得,x+2014<-2,
即x<-2016,
故选:C.
得:2xf(x)+x2f′(x)<x3,
即[x2f(x)]′<x3<0,
令F(x)=x2f(x),
则当x<0时,
得F′(x)<0,即F(x)在(-∞,0)上是减函数,
∴F(x+2014)=(x+2014)2f(x+2014),F(-2)=4f(-2),
即不等式等价为F(x+2014)-F(-2)>0,
∵F(x)在(-∞,0)是减函数,
∴由F(x+2014)>F(-2)得,x+2014<-2,
即x<-2016,
故选:C.
点评:本题主要考查不等式的解法,利用条件构造函数,利用函数单调性和导数之间的关系是解决本题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
已知某算法的流程图如图所示,若输入x=7,y=6,则输出的有序数对为( )
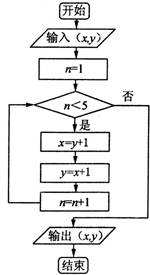

| A、(13,14) |
| B、(12,13) |
| C、(14,13) |
| D、(13,12) |
已知△ABC外接圆的半径为1,圆心为O,且
+
=2
,|
|=|
|,则
•
的值是( )
| CA |
| BA |
| OA |
| OA |
| AB |
| CA |
| BC |
| A、3 | B、2 | C、-2 | D、-3 |
若P为△ABC内一点,且
+
+2
=
,在△ABC内随机撒一颗豆子,则此豆子落在△PBC内的概率为( )
| PB |
| PC |
| PA |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
棱长均为3三棱锥S-ABC,若空间一点P满足
=x
+y
+z
(x+y+z=1)则|
|的最小值为( )
| SP |
| SA |
| SB |
| SC |
| SP |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
设z=1-i(i是虚数单位),则复数
的虚部是( )
| 2 |
| z |
| A、1 | B、-1 | C、i | D、-i |