题目内容
四面体S-ABC中，各个侧面都是边长为a的正三角形，则异面直线SA与BC所成的角等于（ ）
| A、90° | B、60° |
| C、45° | D、30° |
考点：异面直线及其所成的角
专题：计算题,空间角
分析：取BC中点O，连接SO，AO，则SO⊥BC，AO⊥BC，可得BC⊥平面SAO，即可得出结论．
解答：
解：取BC中点O，连接SO，AO，则SO⊥BC，AO⊥BC，
∵SO∩AO=O，
∴BC⊥平面SAO，
∵SA?平面SAO，
∴BC⊥SA，
∴异面直线SA与BC所成的角等于90°．
故选：A．
解：取BC中点O，连接SO，AO，则SO⊥BC，AO⊥BC，∵SO∩AO=O，
∴BC⊥平面SAO，
∵SA?平面SAO，
∴BC⊥SA，
∴异面直线SA与BC所成的角等于90°．
故选：A．
点评：本题考查异面直线及其所成的角，考查学生分析解决问题的能力，比较基础．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
已知a=20.6，b=log0.62，c=0.62，则a，b，c的大小关系是（ ）
| A、a＞b＞c |
| B、a＞c＞b |
| C、b＞a＞c |
| D、b＞c＞a |
已知函数f（x）是R上的增函数，A（0，-1），B（3，1）是其图象上的两点，那|f（x）|＜1的解集是（ ）
| A、（-∞，-1]∪[3，+∞） |
| B、（0，3） |
| C、（-3，0） |
| D、（-∞，0]∪[1，+∞） |
“成都七中”四个字按逆时针排列在1，2，3，4号位置如图所示：，第一次前后排调位，第二次左右调位，依次交替进行下去，那么第2014次互换后，“7”字对应的位置是（ ）
| A、编号1 | B、编号2 |
| C、编号3 | D、编号4 |
函数f（x）=Asin（ωx+φ）（其中ω＞0，|φ|＜| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
请根据所给的图形，把空白的之处填写完整．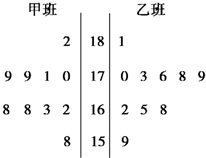
随机抽取某中学甲、乙两班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图如图．