题目内容
已知
＜x＜
，sinx-cosx=
，求值：
（Ⅰ）sinx+cosx；
（Ⅱ）3sin2x+cos2x-4sinxcosx．
| π |
| 4 |
| π |
| 2 |
| 1 |
| 5 |
（Ⅰ）sinx+cosx；
（Ⅱ）3sin2x+cos2x-4sinxcosx．
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：（Ⅰ）已知等式两边平方，利用完全平方公式及同角三角函数间基本关系化简求出2sinxcosx的值，再利用完全平方公式及同角三角函数间的基本关系化简，开方即可求出sinx+cosx的值；
（Ⅱ）由（Ⅰ）求出sinx与cosx的值，代入原式计算即可求出值．
（Ⅱ）由（Ⅰ）求出sinx与cosx的值，代入原式计算即可求出值．
解答：
解：（Ⅰ）∵sinx-cosx=
，
∴（sinx-cosx）2=
，即1-2sinxcosx=
，
整理得：2sinxcosx=
，
∴（sinx+cosx）2=1+2sinxcosx=
，
∵
＜x＜
，
∴（sinx+cosx）＞0，
∴sinx+cosx=
；
（Ⅱ）由（Ⅰ）得：sinx=
，cosx=
，
则原式=3×
+
-4×
×
=
．
| 1 |
| 5 |
∴（sinx-cosx）2=
| 1 |
| 25 |
| 1 |
| 25 |
整理得：2sinxcosx=
| 24 |
| 25 |
∴（sinx+cosx）2=1+2sinxcosx=
| 49 |
| 25 |
∵
| π |
| 4 |
| π |
| 2 |
∴（sinx+cosx）＞0，
∴sinx+cosx=
| 7 |
| 5 |
（Ⅱ）由（Ⅰ）得：sinx=
| 4 |
| 5 |
| 3 |
| 5 |
则原式=3×
| 16 |
| 25 |
| 9 |
| 25 |
| 4 |
| 5 |
| 3 |
| 5 |
| 9 |
| 25 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
已知函数f（x）是R上的增函数，A（0，-1），B（3，1）是其图象上的两点，那|f（x）|＜1的解集是（ ）
| A、（-∞，-1]∪[3，+∞） |
| B、（0，3） |
| C、（-3，0） |
| D、（-∞，0]∪[1，+∞） |
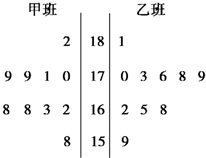随机抽取某中学甲、乙两班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图如图．