题目内容
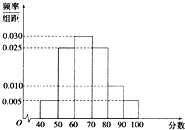某校从高一年级学生中随机抽取部分学生，将他们的模块测试成绩分成6组：[40、50），[50、60），[60、70），[70、80），[80、90），[90、100]加以统计，得到如图所示的频率分布直方图．已知高一年级共有学生600名，据此估计，该模块测试成绩不少于60分的学生人数为（ ）| A、588 | B、420 |
| C、450 | D、120 |
考点：频率分布直方图
专题：概率与统计
分析：根据频率分布直方图，求出该模块测试成绩不少于60分的频率是多少，再求出对应的学生人数是多少．
解答：
解：根据频率分布直方图，得；
该模块测试成绩不少于60分的频率是
1-（0.005+0.025）×10=0.7，
∴对应的学生人数是600×0.7=420．
故选：B．
该模块测试成绩不少于60分的频率是
1-（0.005+0.025）×10=0.7，
∴对应的学生人数是600×0.7=420．
故选：B．
点评：本题考查了频率分布直方图的应用问题，解题时应结合频率分布直方图，进行解答，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
将正方体截取一个四棱锥后得到的几何体如图所示，则有关该几何体的三视图表述正确的是（ ）| A、正视图与俯视图形状完全相同 |
| B、侧视图与俯视图形状完全相同 |
| C、正视图与侧视图形状完全相同 |
| D、正视图、侧视图与俯视图形状完全相同 |
把直线l1：x+3y-1=0沿x轴正方向平移1个单位后得到直线l2，又直线l与直线l2关于x轴对称，那么直线l的方程是（ ）
| A、x-3y+2=0 |
| B、x-3y-4=0 |
| C、x-3y-2=0 |
| D、x-3y+4=0 |
设曲线y=x2-2x-4lnx的一条切线的斜率小于0，则切点的横坐标的取值范围是（ ）
| A、（-1，2） |
| B、（-1，0）∪（2，+∞） |
| C、（0，2） |
| D、（0，+∞） |
当x∈[-2π，-
π]时，化简
+
等于（ ）
| 3 |
| 2 |
| 1+sinx |
| 1-sinx |
A、-2sin
| ||||
B、-2cos
| ||||
C、-2sin
| ||||
D、2cos
|
对于不重合的两平面α，β，给定下列条件：
①存在平面γ，使得α，β都垂直于γ；
②存在平面γ，使得α，β都平行于γ；
③存在直线l?α，m?β，使得l∥m；
④存在异面直线l，m，使得l∥α，l∥β，m∥α，m∥β．
其中可以判定α，β平行的条件有（ ）
①存在平面γ，使得α，β都垂直于γ；
②存在平面γ，使得α，β都平行于γ；
③存在直线l?α，m?β，使得l∥m；
④存在异面直线l，m，使得l∥α，l∥β，m∥α，m∥β．
其中可以判定α，β平行的条件有（ ）
| A、①③ | B、②④ | C、② | D、①④ |
有下列关系：
①曲线上的点与该点的坐标之间的关系；
②苹果的产量与气候之间的关系；
③森林中的同一种树木，其横截面直径与高度之间的关系；
④学生与其学校之间的关系．
其中有相关关系的是（ ）
①曲线上的点与该点的坐标之间的关系；
②苹果的产量与气候之间的关系；
③森林中的同一种树木，其横截面直径与高度之间的关系；
④学生与其学校之间的关系．
其中有相关关系的是（ ）
| A、①② | B、②④ | C、③④ | D、②③ |
设
、
都是非零向量，下列四个条件中，一定能使
+
=
成立的是（ ）
| a |
| b |
| ||
|
|
| ||
|
|
| 0 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|