题目内容
1.函数y=$\sqrt{\sqrt{3}-tan2x}$的定义域是($\frac{kπ}{2}$-$\frac{π}{4}$,$\frac{kπ}{2}$+$\frac{π}{6}$].分析 根据二次根式以及三角函数的性质求出函数的定义域即可.
解答 解:由题意得:
$\sqrt{3}$-tan2x≥0,
∴kπ-$\frac{π}{2}$<2x≤kπ+$\frac{π}{3}$,
解得:$\frac{kπ}{2}$-$\frac{π}{4}$<x≤$\frac{kπ}{2}$+$\frac{π}{6}$,
故答案为:($\frac{kπ}{2}$-$\frac{π}{4}$,$\frac{kπ}{2}$+$\frac{π}{6}$].
点评 本题考查了求函数的定义域问题,考查二次根式以及三角函数的性质,是一道基础题.

练习册系列答案
相关题目
11.圆C1:x2+y2=1与圆C2:x2+(y-2)2=1的位置关系是( )
| A. | 两圆相交 | B. | 两圆内切 | C. | 两圆相离 | D. | 两圆外切 |
12.若a>0,则函数y=ax-1+1的图象经过定点( )
| A. | (1,2) | B. | (2,1) | C. | (0,1+$\frac{1}{a}$) | D. | (2,1+a) |
16.某小区的绿化建设有如下统计数据:
如果以后几年继续依次建设速度发展绿化,那么到哪一年该小区的绿化覆盖率可达到24%?
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 绿化覆盖率(%) | 18.0 | 18.6 | 19.2 | 19.8 | 20.4 |
16.如图,在平行六面体ABCD-A′B′C′D′中,若$\overrightarrow{AB}=\vec a$,$\overrightarrow{AD}=\overrightarrow b$,$\overrightarrow{AA'}=\overrightarrow c$,则$\overrightarrow{BM}$=( )
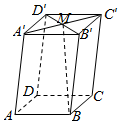

| A. | $-\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | B. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | C. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ | D. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ |