题目内容
在△ABC中,角A、B、C的对边分别为a,b,c,
=
.
(Ⅰ)求角B的大小;
(Ⅱ)求函数f(x)=sinx•cos(x+B)+
(x∈[0,
])的值域.
| tanB |
| tanC |
| 2a-c |
| c |
(Ⅰ)求角B的大小;
(Ⅱ)求函数f(x)=sinx•cos(x+B)+
| ||
| 4 |
| π |
| 2 |
考点:三角函数中的恒等变换应用,同角三角函数基本关系的运用
专题:三角函数的图像与性质,解三角形
分析:(Ⅰ)△ABC中,由正弦定理和三角函数的恒等变换,求出cosB的值,即得角B;
(Ⅱ)利用三角恒等变换,把f(x)化为
sin(2x+
),求出2x+
的取值范围,即得f(x)的值域.
(Ⅱ)利用三角恒等变换,把f(x)化为
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
解答:
解:(Ⅰ)△ABC中,∵
=
,
∴
=
;
又sinC>0,
∴sinBcosC=2sinAcosB-sinCcosB,
∴sin(B+C)=2sinAcosB=sinA,
∴cosB=
,
∴B=
;
(Ⅱ)∵f(x)=sinx•cos(x+
)+
=
sinxcosx-
sin2x+
=
sin2x+
cos2x
=
sin(2x+
),
∵x∈[0,
],
∴2x+
∈[
,
],
∴-
≤sin(2x+
)≤1;
∴f(x)的值域为[-
,
].
| tanB |
| tanC |
| 2a-c |
| c |
∴
| sinBcosC |
| cosBsinC |
| 2sinA-sinC |
| sinC |
又sinC>0,
∴sinBcosC=2sinAcosB-sinCcosB,
∴sin(B+C)=2sinAcosB=sinA,
∴cosB=
| 1 |
| 2 |
∴B=
| π |
| 3 |
(Ⅱ)∵f(x)=sinx•cos(x+
| π |
| 3 |
| ||
| 4 |
=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
=
| 1 |
| 4 |
| ||
| 4 |
=
| 1 |
| 2 |
| π |
| 3 |
∵x∈[0,
| π |
| 2 |
∴2x+
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
∴-
| ||
| 2 |
| π |
| 3 |
∴f(x)的值域为[-
| ||
| 4 |
| 1 |
| 2 |
点评:本题考查了正弦定理和三角恒等变换的应用问题,解题时应根据三角恒等变换公式和正弦定理进行化简与求值,是综合性题目.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
用0,3,5,6,7,8组成无重复数字的五位数,其中能被3整除的五位数有( )
| A、96个 | B、48个 |
| C、192个 | D、240个 |
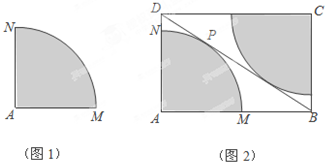 某中学校园内原有一块四分之一圆面形状的草坪AMN(图1),其中AM=AN=8m,∠MAN=90°.今年暑假整治校园环境时,为美观起见,学校设计将原有草坪扩大,具体实施方案是:从圆弧上一点P作圆弧的切线BD,分别与AM,AN的延长线交于B,D,并以AB,AD为邻边构造矩形ABCD,再以C为圆心制作一块与AMN形状相同的草坪,构成矩形绿地ABCD(图2).
某中学校园内原有一块四分之一圆面形状的草坪AMN(图1),其中AM=AN=8m,∠MAN=90°.今年暑假整治校园环境时,为美观起见,学校设计将原有草坪扩大,具体实施方案是:从圆弧上一点P作圆弧的切线BD,分别与AM,AN的延长线交于B,D,并以AB,AD为邻边构造矩形ABCD,再以C为圆心制作一块与AMN形状相同的草坪,构成矩形绿地ABCD(图2).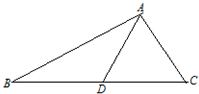 如图,在△ABC中,D是BC上的点,∠C=∠D=2∠DAB,△BAD的面积与△CAD的面积相等,且
如图,在△ABC中,D是BC上的点,∠C=∠D=2∠DAB,△BAD的面积与△CAD的面积相等,且