题目内容
已知P为三角形ABC内部任一点(不包括边界),满足(
-
)•(
+
-2
)=0,则△ABC必定是( )
| PB |
| PA |
| PB |
| PA |
| PC |
| A、直角三角形 |
| B、等边三角形 |
| C、等腰直角三角形 |
| D、等腰三角形 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由向量的运算和已知条件可得
2-
2=0,即|
|=|
|,可得结论.
| CB |
| CA |
| CB |
| CA |
解答:
解:∵
-
=
=
-
,
+
-2
=
-
+
-
=
+
,
∵(
-
)•(
+
-2
)=0,
∴(
-
)•(
+
)=0,
∴
2-
2=0,即|
|=|
|,
∴△ABC一定为等腰三角形.
故选D.
| PB |
| PA |
| AB |
| CB |
| CA |
| PB |
| PA |
| PC |
| PB |
| PC |
| PA |
| PC |
| CB |
| CA |
∵(
| PB |
| PA |
| PB |
| PA |
| PC |
∴(
| CB |
| CA |
| CB |
| CA |
∴
| CB |
| CA |
| CB |
| CA |
∴△ABC一定为等腰三角形.
故选D.
点评:本题考查向量的三角形法则,向量垂直于数量积的关系以及等腰三角形的定义,属中档题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
已知a=log20.3,b=20.1,c=0.21.3,则a,b,c的大小关系是( )
| A、a<b<c |
| B、a<c<b |
| C、c<a<b |
| D、b<c<a |
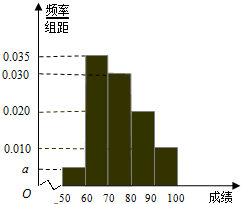 某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下: