题目内容
已知f（x）=（2-a）（x-1）-2lnx，g（x）=xe1-x．且f（x）＞f'（x）对于x∈R恒成立（e为自然对数的底），则（ ）
| A、e2013•f（2014）＞e2014•f（2013） |
| B、e2013•f（2014）=e2014•f（2013） |
| C、e2013•f（2014）＜e2014•f（2013） |
| D、e2013•f（2014）与e2014•f（2013）大小不确定 |
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：先转化为函数y=
的导数形式，再根据导数符号判断函数在R上的增减性，从而得到答案．
| f(x) |
| ex |
解答：
解：解：∵f（x）＞f'（x），
∴f'（x）-f（x）＜0，
∴(
)′=
＜0
从而函数y=
在R上单调递减，
故x=2时函数的值大于x=0时函数的值，
∴
＞
即e2013•f（2014）＜e2014•f（2013）．
故选C．
∴f'（x）-f（x）＜0，
∴(
| f(x) |
| ex |
| ex[f′(x)-f(x)] |
| e2x |
从而函数y=
| f(x) |
| ex |
故x=2时函数的值大于x=0时函数的值，
∴
| f(2013) |
| e2013 |
| f(2014) |
| e2014 |
即e2013•f（2014）＜e2014•f（2013）．
故选C．
点评：本题主要考查函数的单调性与其导函数的正负情况之间的关系，即导函数大于0时原函数单调递增，当导函数小于0时原函数单调递减．解题时注意函数的构造．
练习册系列答案
相关题目
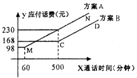电信局为满足不同客户的需要，设有A、B两种优惠方案，这两种方案应付话费（元）与通话时间（分钟）之间的关系如图（MN∥CD），若通话时间为500分钟，则应选择哪种方案更优惠（ ）| A、方案A | B、方案B |
| C、两种方案一样优惠 | D、不能确定 |
若数列{an}为等差数列，ap=q，aq=p（p≠q），则ap+q=（ ）
| A、p+q | ||
| B、0 | ||
| C、-（p+q） | ||
D、
|
已知函数f（x）=ax2+bx+c（a＞0），且f（-1）=f（3），则（ ）
A、f（-3）＜c＜f（
| ||
B、f（
| ||
C、f（
| ||
D、c＜f（
|