题目内容
已知函数f(x)=
有下列说法:
①函数f(x)对任意x1,x2∈[0,+∞),都有|f(x1)-f(x2)|≤2成立
②函数f(x)在[
(4n-3),
(4n-1)](n∈N•)上单调递减;
③函数y=f(x)-log2x+1在(0,+∞)上有3个零点;
④当k∈[
,+∞)时,对任意x>0,不等式f(x)≤
都成立.
其中正确的说法的个数是( )
|
①函数f(x)对任意x1,x2∈[0,+∞),都有|f(x1)-f(x2)|≤2成立
②函数f(x)在[
| 1 |
| 2 |
| 1 |
| 2 |
③函数y=f(x)-log2x+1在(0,+∞)上有3个零点;
④当k∈[
| 8 |
| 7 |
| k |
| x |
其中正确的说法的个数是( )
| A、4 | B、3 | C、2 | D、1 |
考点:分段函数的应用
专题:计算题,作图题,函数的性质及应用
分析:作函数f(x)=
的图象,由图象对四个命题判断.
|
解答:
解:作函数f(x)=
的图象如下,
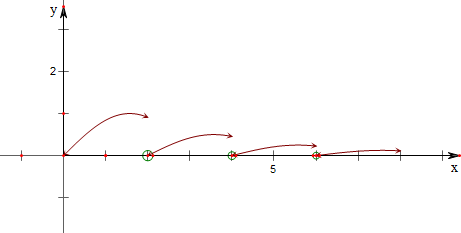
由图可知,
①函数f(x)对任意x1,x2∈[0,+∞),都有|f(x1)-f(x2)|≤2成立,正确;
②函数f(x)在(2n,2n+
],(n∈N)上是增函数,故在[
(4n-3),
(4n-1)](n∈N•)上也单调递增;故不正确;
③函数y=f(x)-log2x+1在(0,+∞)上有3个零点即y=f(x)与y=log2x-1的交点个数,
作y=f(x)与y=log2x-1的图象如下,
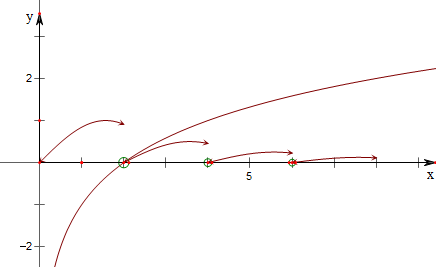
没有交点,故没有零点;故不正确;
④f(x)≤
可化为xf(x)≤k,作y=xf(x)的图象如下,
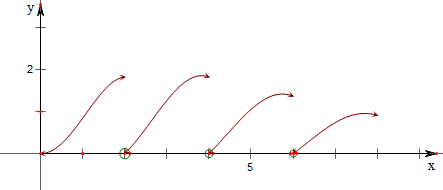
当k∈[
,+∞)时,对任意x>0,不等式f(x)≤
都成立显然不正确.
故选D.
|

由图可知,
①函数f(x)对任意x1,x2∈[0,+∞),都有|f(x1)-f(x2)|≤2成立,正确;
②函数f(x)在(2n,2n+
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
③函数y=f(x)-log2x+1在(0,+∞)上有3个零点即y=f(x)与y=log2x-1的交点个数,
作y=f(x)与y=log2x-1的图象如下,

没有交点,故没有零点;故不正确;
④f(x)≤
| k |
| x |

当k∈[
| 8 |
| 7 |
| k |
| x |
故选D.
点评:本题考查了函数的图象的作法与应用,属于中档题.

练习册系列答案
相关题目
已知数列{an}是等差数列,且an=2n+1,则公差d=( )
| A、1 | B、2 | C、3 | D、-2 |
 如图,已知抛物线C:x2=4y,过焦点F任作一条直线与C相交于A,B两点,过点B作y轴的平行线与直线AO相交于点D(O为坐标原点).
如图,已知抛物线C:x2=4y,过焦点F任作一条直线与C相交于A,B两点,过点B作y轴的平行线与直线AO相交于点D(O为坐标原点).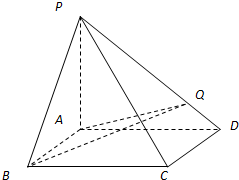 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是矩形,已知PA=AD=2AB=4,Q是线段PD上一点,PC⊥AQ.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是矩形,已知PA=AD=2AB=4,Q是线段PD上一点,PC⊥AQ.