题目内容

函数y=
3x+3
2x+1
的值域为
 
．
考点：函数的值域
专题：函数的性质及应用
分析：分离常数可得y=
3
2
+
3
2(2x+1)
，由
3
2(2x+1)
≠0可得y≠
3
2
，可得函数的值域．
解答： 解：由题意可得y=
3x+3
2x+1

=
3
2
(2x+1)+
3
2
2x+1
=
3
2
+
3
2(2x+1)
，
∵
3
2(2x+1)
≠0，∴y≠
3
2
，
∴函数的值域为：{y|y≠
3
2
}
故答案为：{y|y≠
3
2
}
点评：本题考查函数值域的求解，分离常数是解决问题的关键，属基础题．
练习册系列答案
相关题目
已知函数f（x）=x2+2（a-1）x+2．
（1）当a=2时，写出f（x）的单调区间；
（2）若该函数的单调递减区间为（-∞，4]，求实数a的值；
（3）若该函数在（-∞，4]上单调递减，求实数a的取值范围．
投掷两颗相同的正方体骰子（骰子质地均匀，且各个面上依次标有点数1、2、3、4、5、6）一次，则两颗骰子向上点数之积等于6的概率为
 
．
已知函数y=f（x），x∈R，
（1）y=f（x-2）与y-f（2-x）的图象关于直线 x=2对称；
（2）有下列4个命题：
①若f（1+2x）=f（1-2x），则f（x）的图象关于直线x=1对称；
②f（2x+5）=f（2x）则5是y=f（x）的周期；
③若f（x）为偶函数，且f（2+x）=-f（x），则f（x）的图象关于直线x=2对称；
④若f（x）为奇函数，且f（x）=f（-x-2），则f（x）的图象关于直线x=1对称．
其中正确的命题为_
 
．
已知集合A={1，2，3，4，5}，从A的非空子集中任取一个，该集合中所有元素之和为奇数的概率是
 
．
执行如图所示的程序框图，若输入如下四个函数：
①f（x）=sinx，②f（x）=cosx，③f（x）=
1
x
，④f（x）=x2，
则输出的函数是（　　）
A、f（x）=sinx
B、f（x）=cosx
C、f（x）=
1
x
D、f（x）=x2
给出下列五个命题：
①随机事件的概率不可能为0；
②事件A，B中至少有一个发生的概率一定比A，B中恰有一个发生的概率大；
③掷硬币100次，结果51次出现正面，则出现正面的概率是
51
100
；
④互斥事件不一定是对立事件，对立事件一定是互斥事件；
⑤如果事件A与B相互独立，那么A与
.
B
，
.
A
与B，
.
A
与
.
B
也都相互独立
其中真命题的个数是（　　）
A、1B、2C、3D、4
在正方体ABCD-A1B1C1D1中，M，N分别C1D1，BC是的中点，则下列判断正确的是（　　）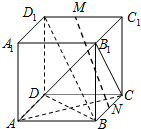
A、MN∥BD1
B、MN⊥AB1
C、MN∥平面BDD1
D、MN⊥平面AB1C
某商店购进一批单价为16元的日用品，销售一段时间后，为了获得更多的利益，商店决定提高商品的销售价格，经实际的销售过程发现，若按每件18元销售，每月能销售1200件，若按每件22元销售，每月可以销售400件，已知销售量y（件）与销售价格x（元）之间的关系是一次函数关系，求解下列问题：
（1）写出销售量y（件）与销售价格x（元）之间的函数关系式；
（2）如何定价能使每月的销售利润最大，并求最大利润的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网