题目内容
10.已知等差数列{an}的前n项和为Sn,若$\frac{{S}_{6}}{{S}_{3}}$=3,则$\frac{{S}_{12}}{{S}_{9}}$=( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | 2 | D. | 3 |
分析 由已知条件利用等差数列前n项和公式推导出a1=2d,由此能求出$\frac{{S}_{12}}{{S}_{9}}$的值.
解答 解:∵等差数列{an}的前n项和为Sn,$\frac{{S}_{6}}{{S}_{3}}$=3,
∴$\frac{6{a}_{1}+\frac{6×5}{2}d}{3{a}_{1}+\frac{3×2}{2}d}$=3,整理,得a1=2d,
∴$\frac{{S}_{12}}{{S}_{9}}$=$\frac{12{a}_{1}+\frac{12×11}{2}d}{9{a}_{1}+\frac{9×8}{2}d}$=$\frac{12{a}_{1}+66d}{9{a}_{1}+36d}$=$\frac{5}{3}$.
故选:B.
点评 本题考查等差数列的前12项和与前9项和的比值的求法,是基础题,解题时要注意等差数列的前n项和公式的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.函数y=$\frac{1}{{x}^{2}+2}$的值域为( )
| A. | R | B. | [$\frac{1}{2}$,+∞) | C. | (-∞,$\frac{1}{2}$] | D. | (0,$\frac{1}{2}$] |
15.-$\frac{2015π}{6}$是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
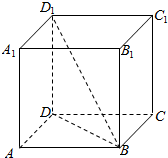 在正方体ABCD-A1B1C1D1中,对角线BD1分别与平面AC,平面BC1,平面BA1所成的角,并求这些角的余弦值.
在正方体ABCD-A1B1C1D1中,对角线BD1分别与平面AC,平面BC1,平面BA1所成的角,并求这些角的余弦值.