题目内容
20．函数f（x）=x2+bx+1的最小值是0，则实数b=±2．分析 直接利用二重身的最值列出方程求解即可．
解答 解：函数f（x）=x2+bx+1的最小值是0，
可得$\frac{4-{b}^{2}}{4}=0$，解得b=±2．
故答案为：±2．
点评 本题考查函数的最值，二次函数的性质的应用，考查计算能力．
练习册系列答案
相关题目
10．已知等差数列{an}的前n项和为Sn，若$\frac{{S}_{6}}{{S}_{3}}$=3，则$\frac{{S}_{12}}{{S}_{9}}$=（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{5}{3}$ | C． | 2 | D． | 3 |
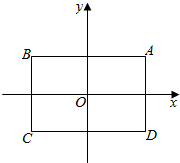如图，坐标原点O为矩形ABCD的对称中心，顶点A的坐标为（1，t），AB∥x轴，矩形A′B′C′D′与矩形ABCD是位似图形，点O为位似中心，点A′，B′分是点A，B的对应点，$\frac{A′B′}{AB}$=k．已知关于x，y的元二次一次方程$\left\{\begin{array}{l}{mnx+y=3n+1}\\{3x+y=4}\end{array}\right.$（m，n是实数）无解，在以m，n为坐标（记为m，n）的所有的点中，若有且只有一个点落在矩形A′B′C′D′的边上．则k•t的值等于1．
8．设集合A={1，2}，集合B={2，3，5}，则A∩B等于（ ）
| A． | {2} | B． | {1，2，3，5} | C． | {1，3} | D． | {2，5} |
12．下列各关系中，不正确的是 （ ）
| A． | {正方形}⊆{矩形} | B． | a⊆{a，b，c} | C． | R?Q | D． | {1，2，3}={3，2，1} |