题目内容
19.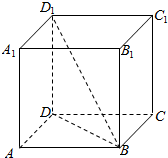 在正方体ABCD-A1B1C1D1中,对角线BD1分别与平面AC,平面BC1,平面BA1所成的角,并求这些角的余弦值.
在正方体ABCD-A1B1C1D1中,对角线BD1分别与平面AC,平面BC1,平面BA1所成的角,并求这些角的余弦值.
分析 利用正方体的结构特征和线面角的定义,结合勾股定理求解.
解答 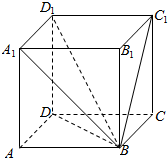 解:如图,在正方体ABCD-A1B1C1D1中,
解:如图,在正方体ABCD-A1B1C1D1中,
设棱长为1,由BD=BC1=$\sqrt{2}$,BD1=$\sqrt{3}$,
∵D1D⊥平面AC,∴对角线BD1与平面AC所成的角为∠DBD1,
cos∠DBD1=$\frac{BD}{B{D}_{1}}$=$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{6}}{3}$.
∵D1C1⊥平面BC1,∴对角线BD1与平面BC1所成的角为∠C1BD1,
cos∠C1BD1=$\frac{B{C}_{1}}{B{D}_{1}}$=$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{6}}{3}$,
∵A1D1⊥平面BA1,∴对角线BD1分别与平面BA1所成的角为∠A1BD1,
cos∠A1BD1=$\frac{{A}_{1}B}{B{D}_{1}}$=$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{6}}{3}$.
点评 本题考查线面角的判断及其余弦值的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
10.已知P是双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1上的任意一点,F1,F2是它的左右焦点,且|PF1|=5,则|PF2|=( )
| A. | 1 | B. | 9 | C. | 1或9 | D. | 9或5 |
9.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点分别为F1、F2,过F2的直线交双曲线的渐近线于A、B两点,若F1A⊥F2A,且$\overrightarrow{{F}_{2}B}$=3$\overrightarrow{A{F}_{2}}$,则双曲线的离心率为( )
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
10.已知等差数列{an}的前n项和为Sn,若$\frac{{S}_{6}}{{S}_{3}}$=3,则$\frac{{S}_{12}}{{S}_{9}}$=( )
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | 2 | D. | 3 |
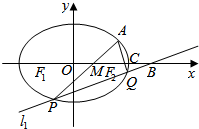 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点为F1、F2,且椭圆E过点(0,$\sqrt{3}$),($\sqrt{3}$,-$\frac{\sqrt{6}}{2}$),点A是椭圆上位于第一象限的一点,且△AF1F2的面积S△${\;}_{A{F}_{1}{F}_{2}}$=$\sqrt{3}$.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点为F1、F2,且椭圆E过点(0,$\sqrt{3}$),($\sqrt{3}$,-$\frac{\sqrt{6}}{2}$),点A是椭圆上位于第一象限的一点,且△AF1F2的面积S△${\;}_{A{F}_{1}{F}_{2}}$=$\sqrt{3}$.