题目内容
2．四棱锥P-ABCD中，底面ABCD是平行四边形，点E是PD上的点，且PE=2DE，在PC上找一点F，使得BF∥平面ACE．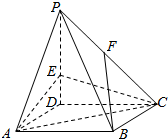
分析 连结BD交AC于O点，连结OE，过B点作OE的平行线交PD于点G，过G作GF∥CE，交PC于点F，连结BF，由此能求出存在点F是PC中点时，使BF∥面AEC．
解答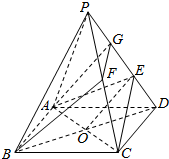 
解：连结BD交AC于O点，连结OE，过B点作OE的平行线交PD于点G，
过G作GF∥CE，交PC于点F，连结BF．
∵BG∥OE，BG?面AEC，OE?面AEC，
∴BG∥面AEC．
同理GF∥面AEC．
又BG∩GF=G，
∴面BFG∥面AEC，BF?面BFG．
∴BF∥面AEC．
下面求一下点F在PC上的具体位置．
∵BG∥OE，O是BD中点，
∴E是GD中点．
又∵PE：ED=2：1，
∴G是PE中点．
而GF∥CE，∴F为PC中点．
综上，存在点F是PC中点时，使BF∥面AEC．
点评 本题考查满足线面平行的点的位置的确定，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
导学全程练创优训练系列答案
相关题目
12．（重点中学做）不等式$\frac{4}{x-1}$≤x-1的解集是（ ）
| A． | （-∞，-1]∪（1，3] | B． | [-1，1）∪[3，+∞） | C． | （-∞，-1]∪[3，+∞） | D． | [-1，1）∪（1，3] |
13．已知一个正方形的边长为6，现用直径为2的硬币投掷到此正方方形上，则硬币落下后与此正方形的边有公共点的概率为（ ）
| A． | $\frac{4}{9}$ | B． | $\frac{5}{9}$ | C． | $\frac{1}{3}$ | D． | $\frac{2}{3}$ |