题目内容
若函数y＝lg(3－4x＋x2)的定义域为M.当x∈M时，求f(x)＝2x＋2－3×4x的最值及相应的x的值．
要使函数y＝lg(3－4x＋x2)有意义，应有3－4x＋x2>0，
解得x<1或x>3，∴M＝{x<1或x>3}．
f(x)＝2x＋2－3×4x＝4×2x－3×(2x)2，
令2x＝t，∵x<1或x>3，∴t>8或0<t<2.
∴y＝4t－3t2＝－3(t－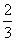
)2＋
(t>8或0<t<2)，
由二次函数性质可知，
当0<t<2时，f(x)∈(－4，]；
当t>8时，f(x)∈(－∞，－160)；
当2x＝t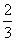＝，即x＝log2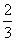时，y＝.
综上可知，当x＝log2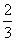时，f(x)取到最大值为，无最小值.
练习册系列答案
阅读快车系列答案
相关题目
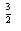＝a3；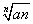
＝|a|(n>1，n∈N＋，n为偶数)；
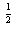－(3x－7)0的定义域是{x|x≥2且x≠
}；
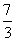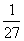，则x＋y＝7.
的定义域为R，则实数m的取值范围是( )
] B．(0，
，角α的终边经过点P(sin2θ，sin4θ)，则
的值为( )