题目内容
已知椭圆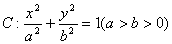 的离心率为
的离心率为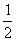 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线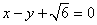 相切。
相切。
(I)求椭圆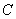 的方程;
的方程;
(II)设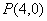 ,
,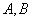 是椭圆
是椭圆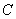 上关于
上关于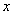 轴对称的任意两个不同的点,连接
轴对称的任意两个不同的点,连接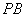 交椭圆
交椭圆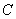 于另一点
于另一点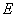 ,证明直线
,证明直线 与
与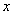 轴相交于定点
轴相交于定点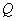 ;
;
(Ⅲ)在(II)的条件下,过点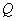 的直线与椭圆
的直线与椭圆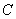 交于
交于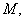
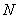 两点,求
两点,求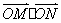 的取值范围.
的取值范围.
解:(I)
(II)由题意可知 存在且不为0.
存在且不为0.
 消
消 得
得 ,
,
令 则
则 ,
,
所以
令 ,由韦达定理化简得
,由韦达定理化简得 ,
,
所以直线 与
与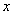 轴相交于定点
轴相交于定点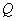
 .
.
(Ⅲ)  当
当 为椭圆长轴的两个顶点时,
为椭圆长轴的两个顶点时,

 消
消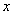 得:
得:
令 .
.
则
所以

练习册系列答案
相关题目
 的焦点
的焦点 直线与
直线与 交于
交于 两点.
两点.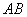 中点
中点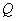 的轨迹方程;
的轨迹方程; 是抛物线
是抛物线 与抛物线C的准线
与抛物线C的准线 分别交于点
分别交于点 ,
, 的值.
的值. 图像与函数
图像与函数
 图像所有交点的纵坐标之和 .
图像所有交点的纵坐标之和 .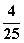 B.
B.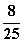 C.
C.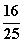 D.
D.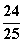
 且
且 ,函数
,函数 若数列
若数列 满足
满足
 ,且
,且
 集合
集合 ,则集合
,则集合 等于( )
等于( ) B.
B.  C.
C.  D.
D. 
 秒内的任何时刻,两条不相关的短信机会均等地进人同一部手机,若这两条短信进人手机的时间之差小于
秒内的任何时刻,两条不相关的短信机会均等地进人同一部手机,若这两条短信进人手机的时间之差小于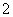 秒,手机就会受到干扰,则手机受到干扰的概率为( )
秒,手机就会受到干扰,则手机受到干扰的概率为( )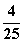 B.
B.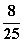 C.
C.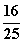 D.
D.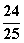
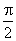 )∪[
)∪[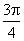 ,π)
,π) D.
D. lg 2
lg 2