题目内容

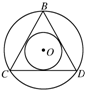
在半径为1的圆内任一点为中点作弦，求弦长超过圆内接等边三角形边长的概率．
考点：几何概型
专题：概率与统计
分析：求出弦长超过圆内接等边三角形边长的区域，则符合条件的点必须在内接等边三角形的内切圆内，所求概率为两圆的面积比，由几何槪型的概率公式即可得到结论．
解答： 解：由题意可得：符合条件的点必须在内接等边三角形的内切圆内，
因为两圆的圆心相同，大圆的半径为1，故内接正三角形的边长为
3
，
故内接等边三角形的内切圆半径为
1
2
，
故弦长超过圆内接等边三角形边长的概率P=
S小圆
S大圆
=
π×(
1
2
)2
π×12
=
1
4
．
点评：本题主要考查几何槪型的概率计算，求出对应的面积是解决本题的关键．
练习册系列答案
相关题目
已知函数f（x）=x2+2bx的图象在点A（0，f（0））处的切线l与直线x-y+3=0平行，若数列{
1
f(n)
}的前n项和为Sn，则S2011的值为（　　）
A、
2011
2012
B、
2013
2012
C、
2012
2013
D、
2010
2011
在数列{an}中，a1=-
2
3
，其前n项和为Sn满足Sn+
1
Sn
=an-2，（n≥2）．
（1）计算S1、S2、S3、S4； 
（2）猜想Sn的表达式，并加以证明．
在平面直角坐标系xOy中，过点P（-4，0）作直线交椭圆C：
x2
a2
+
y2
3
=1（a＞0）于A，B两点，设点B关于x轴的对称点为B′，点F（-1，0）为椭圆C的左焦点，且
PB
=λ
PA
（λ＞1）．
（1）求实数a的值；
（2）若λ=2，求线段BB′的长；
（3）证明：
B′F
=λ
FA
．
已知各项均为正数的数列{an}，满足
a
2
n+1
-an+1an-2
a
2
n
=0（n∈N*），且a1=2．
（1）求数列{an}的通项公式；
（2）设bn=an•log
1
2
an，若bn的前n项和为Sn，求Sn；
（3）在（2）的条件下，求使Sn+n•2n+1＞50成立的正整数n的最小值．
2014年年初，某微小企业开发某项新产品，先期投入5万元启动资金，计划两年内逐月增加投入，已知2014年1月份投入资金0.1万元，以后每月比上个月多投入资金0.1万元，若该产品每个月的利润组成数列{an}，an=
n
5
，   n∈[1，12]，n∈N*
5
2
，   n∈[13，24]，n∈N*
．
（Ⅰ）求前n个月的利润总和；
（Ⅱ）设第n个月的利润率bn=
第n月利润
前n-1个月投入的资金总和
，求两年内哪一个月的利润率最大？并求出最大利润率．
在△ABC中，角A，B，C所对应的边分别为a，b，c．若a，b是方程x2-2
3
x+2=0的两根，且2cos（A+B）=1．
（1）求角C的度数；
（2）求c；
（3）求△ABC的面积．
学校在高二开设了当代战争风云、投资理财、汽车模拟驾驶与保养、硬笔书法共4门选修课，每个学生必须且只需从4门选修课中任选1门选修课选修，对于该年级的甲、乙、丙3名学生：求：
（1）甲选战争风云课而且乙选投资理财课的概率；
（2）这3名学生选择的选修课互不相同的概率；
（3）投资理财选修课被这3名学生选择的人数X的分布列．
某公司“咨询热线”电话共有10路外线，经长期统计发现，在8点至10点这段时间内，外线电话同时打入情况如表所示：
电话同时打入数ξ 0 1 2 3 4 5 6 7 8 9 10
概率P 0.13 0.35 0.27 0.14 0.08 0.02 0.01 0 0 0 0
（1）若这段时间内，公司只安排了2位接线员（一个接线员一次只能接一个电话）．
①求至少一路电话不能一次接通的概率；
②在一周五个工作日中，如果有三个工作日的这一时间内至少一路电话不能一次接通，那么公司的形象将受到损害，现用至少一路电话一次不能接通的概率表示公司形象的“损害度”，求这种情况下公司形象的“损害度”；
（2）求一周五个工作日的这一时间内，同时打入的电话数ξ的期望值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网