题目内容
设实数x,y满足约束条件:
,则z=x2+y2的最大值为 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用z的几何意义,利用数形结合,即可得到结论.
解答:
解:作出不等式组对应的平面区域如图:作出不等式组对应的平面区域如图:
则z=x2+y2的几何意义为动点P(x,y)到原点距离的平方的最大值,
由图象可知当P位于点A时,距离最大,
由
,解得
此时zmax=x2+y2=22+82=68.
故答案为:68

则z=x2+y2的几何意义为动点P(x,y)到原点距离的平方的最大值,
由图象可知当P位于点A时,距离最大,
由
|
|
此时zmax=x2+y2=22+82=68.
故答案为:68
点评:本题主要考查线性规划的应用,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
三棱锥P-ABC的四个顶点均在同一球面上,其中△ABC是正三角形,PA⊥平面ABC,PA=2AB=6,则该球的体积为( )
A、16
| ||
B、32
| ||
| C、48π | ||
D、64
|
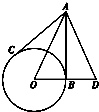 如图,AB、AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于
如图,AB、AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于