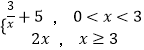Question

【题目】已知向量 =（1，m）， =（2，n）．
（1）若m=3，n=﹣1，且 ⊥（ +λ ），求实数λ的值；
（2）若| + |=5，求 的最大值．

Answer 1

【答案】
（1）解： m=3，n=﹣1时， =（1，3）， =（2，﹣1），

∴ +λ =（1+2λ，3﹣λ），

∵ ⊥（ +λ ），

∴ （ +λ ）=1+2λ+3（3﹣λ）=0，

解得λ=10，

（2）∵ =（1，m）， =（2，n），

∴ + =（3，m+n）， =2+mn，

∵| + |=5，

∴9+（m+n）2=25，

∴（m+n）2=16，

∴ =2+mn≤2+ （m+n）2=6，

当且仅当m=n=2或m=n=﹣2时取等号，

故 的最大值6．

【解析】（1）先计算+λ的坐标，再由已知条件可得含有λ的方程，解方程可得实数λ的值；（2）先计算+的坐标和，再由已知条件可得（m+n）2，进而利用基本不等式可得 的最大值．