Question

【题目】如图，在平面四边形ABCD中，已知∠A= ，∠B= ，AB=6．在AB边上取点E使得BE=1，连结EC，ED，若∠CED= ，EC= ．则CD= ．

Answer 1

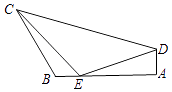
【答案】7
【解析】解：在△CBE中，由余弦定理得CE2=BE2+CB2﹣2BECBcos120°，

即7=1+CB2+CB，解得CB=2．

由余弦定理得CB2=BE2+CE2﹣2BECEcos∠BECcos∠BEC= ，

sin∠BEC= ．

sin∠AED=sin（1200+∠BEC）= ，

cos∠AED= ．

在直角△ADE中，AE=5，cos ，DE=2 ，

在△CED中，由余弦定理得CD2=CE2+DE2﹣2CEDEcos120°=49

∴CD=7．

所以答案是：7