题目内容
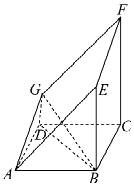
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分别是棱A1B1、AB、A1D1的中点.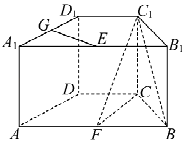
(Ⅰ)求证:GE⊥平面FCC1;
(Ⅱ)求二面角B﹣FC1﹣C的余弦值.
【答案】解:因为AB=4,BC=CD=2,F是棱AB的中点,
所以BF=BC=CF,△BCF为正三角形,因为ABCD为等腰梯形,
所以∠BAD=∠ABC=60°,取AF的中点M,
连接DM,则DM⊥AB,所以DM⊥CD.
以DM,DC,DD1所在直线分别为x,y,z轴建立空间直角坐标系,
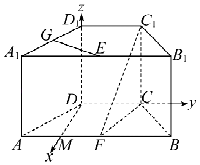
则D(0,0,0), ![]() ,
, ![]() C(0,2,0),C1(0,2,2),
C(0,2,0),C1(0,2,2), ![]() ,
, ![]() ,
, ![]() ,
,
所以 ![]() ,
, ![]() ,
, ![]() .
.
设平面CC1F的法向量为 ![]() ,则
,则 
∴ ![]() 取
取 ![]() .
.
(Ⅰ)证明:GE的方向向量为 ![]() ,
,
∵ ![]() ,∴GE⊥平面FCC1.
,∴GE⊥平面FCC1.
(Ⅱ)解: ![]() ,设平面BFC1的法向量为
,设平面BFC1的法向量为 ![]() ,则
,则 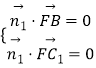
所以 ![]() 取
取 ![]() ,
,
则 ![]() ,
, ![]() ,
, ![]() ,
,
所以 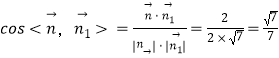 ,由图可知二面角B﹣FC1﹣C为锐角,
,由图可知二面角B﹣FC1﹣C为锐角,
所以二面角B﹣FC1﹣C的余弦值为 ![]() .
.
【解析】(Ⅰ)由题意取AF得中点M,连接DM得出DM⊥CD根据题意,建立空间直角坐标系,利用向量法求解即可得证。(Ⅱ)根据题意建立空间直角坐标系求出各个点的坐标进而求出各个向量的坐标,设出平面BFC1和平面CC1F的法向量,由向量垂直的坐标运算公式可求出法向量,再利用向量的数量积运算公式求出余弦值即可。。
【考点精析】通过灵活运用直线与平面垂直的判定,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想即可以解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案