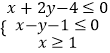题目内容
【题目】已知数列{an}的前n项和为Sn , 且满足Sn=2an﹣2;数列{bn}的前n项和为Tn , 且满足b1=1,b2=2, ![]() .
.
(1)求数列{an}、{bn}的通项公式;
(2)是否存在正整数n,使得 ![]() 恰为数列{bn}中的一项?若存在,求所有满足要求的bn;若不存在,说明理由.
恰为数列{bn}中的一项?若存在,求所有满足要求的bn;若不存在,说明理由.
【答案】
(1)解:由Sn=2an﹣2,则当n≥2时,Sn﹣1=2an﹣1﹣2,
两式相减得:an=2an﹣2an﹣1,则an=2an﹣1,
由S1=2a1﹣2,则a1=2,
∴数列{an}是以2为首项,2为公比的等比数列,则an=2n,
由 ![]() .
.
则 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() ,…,
,…, ![]() =
= ![]() .
. ![]() =
= ![]()
以上各式相乘, ![]() =
= ![]() ,则2Tn=bnbn+1,
,则2Tn=bnbn+1,
当n≥2时,2Tn﹣1=bn﹣1bn,两式相减得:2bn=bn(bn+1﹣bn﹣1),即bn+1﹣bn﹣1=2,
∴数列{bn}的奇数项,偶数项分别成等差数列,
由 ![]() =
= ![]() ,则b3=T2=b1+b2=3,b1+b3=2b2,
,则b3=T2=b1+b2=3,b1+b3=2b2,
∴数列{bn}是以b1=1为首项,1为公差的等差数列,
∴数列{bn}的通项公式bn=n;
(2)当n=1时, ![]() 无意义,
无意义,
设cn= ![]() =
= ![]() ,(n≥2,n∈N*),
,(n≥2,n∈N*),
则cn+1﹣cn= ![]() ﹣
﹣ ![]() =
= ![]() <0,
<0,
即cn>cn+1>1,
显然2n+n+1>2n﹣(n+1),则c2=7>c3=3>c4>…>1,
∴存在n=2,使得b7=c2,b3=c3,
下面证明不存在c2=2,否则,cn= ![]() =2,即2n=3(n+1),
=2,即2n=3(n+1),
此时右边为3的倍数,而2n不可能是3的倍数,故该不等式成立,
综上,满足要求的bn为b3,b7.
【解析】(1)先根据所给的数列前n项和与通项公式求得数列的首项及数列特征,进而求得数列的通项公式;(2)根据(1)可知数列{bn}的通项公式bn=n,结合题意求所给数列为正整数的情况即可;首先判断所给数列的首项值,再判断所给数列的增减性,进而解决此题.

 名校课堂系列答案
名校课堂系列答案【题目】随着“全面二孩”政策推行,我市将迎来生育高峰.今年新春伊始,泉城各医院产科就已经是一片忙碌至今热度不减.卫生部门进行调查统计期间发现各医院的新生儿中,不少都是“二孩”;在市第一医院,共有40个猴宝宝降生,其中10个是“二孩”宝宝;
(Ⅰ)从两个医院当前出生的所有宝宝中按分层抽样方法抽取7个宝宝做健康咨询,
①在市第一医院出生的一孩宝宝中抽取多少个?
②若从7个宝宝中抽取两个宝宝进行体检,求这两个宝宝恰出生不同医院且均属“二孩”的概率;
(II)根据以上数据,能否有85%的把握认为一孩或二孩宝宝的出生与医院有关?
P(k≥k市) | 0.40 | 0.25 | 0.15 | 0.10 |
k市 | 0.708 | 1.323 | 2.072 | 2.706 |
K2= ![]() .
.