题目内容
【题目】已知函数h(x)=﹣|x﹣3|.
(1)若h(x)﹣|x﹣2|≤n对任意的x>0恒成立,求实数n的最小值;
(2)若函数f(x)= 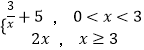 ,求函数g(x)=f(x)+h(x)的值域.
,求函数g(x)=f(x)+h(x)的值域.
【答案】
(1)解:∵h(x)﹣|x﹣2|≤n对任意的x>0恒成立,等价于﹣|x﹣3|﹣|x﹣2|≤n对任意的x>0恒成立,
等价于﹣n≤(|x﹣2|+|x﹣3|)min对任意的x>0.
因为|x﹣2|+|x﹣3|≥|x﹣2﹣(x﹣3)|=1,当且仅当x∈[2,3]时取等号,所以﹣n≤1,得n≥﹣1.
所以实数n的最小值为﹣1.
(2)因为f(x)= 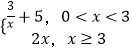 ,g(x)=f(x)+h(x),
,g(x)=f(x)+h(x),
所以g(x)=f(x)﹣|x﹣3|= 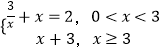 ,
,
当0<x<3时, ![]() =2
=2 ![]() +2,
+2,
当x≥3时,x+3≥6.
综上,g(x)≥2 ![]() +2.
+2.
所以函数g(x)=f(x)+h(x)的值域为[2 ![]() +2,+∞).
+2,+∞).
【解析】(1)使用绝对值不等式求出![]() 的最小值为1,所以n的最小值为-1;(2)根据分段函数,写出在不同区间的解析式,求出各段函数中的值域,综上得出g(x)的值域.
的最小值为1,所以n的最小值为-1;(2)根据分段函数,写出在不同区间的解析式,求出各段函数中的值域,综上得出g(x)的值域.
【考点精析】本题主要考查了函数的值域的相关知识点,需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能正确解答此题.

【题目】某种产品的质量以其质量指标衡量,并依据质量指标值划分等级如表:
质量指标值m | m<185 | 185≤m<205 | M≥205 |
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
(1)根据以上抽样调查的数据,能否认为该企业生产这种产品符合“一、二等品至少要占到全部产品的92%的规定”?
(2)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品的质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值X近似满足X~N(218,140),则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
【题目】随着“全面二孩”政策推行,我市将迎来生育高峰.今年新春伊始,泉城各医院产科就已经是一片忙碌至今热度不减.卫生部门进行调查统计期间发现各医院的新生儿中,不少都是“二孩”;在市第一医院,共有40个猴宝宝降生,其中10个是“二孩”宝宝;
(Ⅰ)从两个医院当前出生的所有宝宝中按分层抽样方法抽取7个宝宝做健康咨询,
①在市第一医院出生的一孩宝宝中抽取多少个?
②若从7个宝宝中抽取两个宝宝进行体检,求这两个宝宝恰出生不同医院且均属“二孩”的概率;
(II)根据以上数据,能否有85%的把握认为一孩或二孩宝宝的出生与医院有关?
P(k≥k市) | 0.40 | 0.25 | 0.15 | 0.10 |
k市 | 0.708 | 1.323 | 2.072 | 2.706 |
K2= ![]() .
.