题目内容
已知F1,F2是双曲线
-
=1(a>0,b>0)的两个焦点,PQ是经过F1且垂直于x轴的双曲线的弦,如果∠PF2Q=90°,则双曲线的离心率( )
| x2 |
| a2 |
| y2 |
| b2 |
A、2
| ||
B、1+
| ||
C、1+
| ||
D、2+2
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据PQ是经过F1且垂直于x轴的双曲线的弦,∠PF2Q=90°,可得|PF1|=|F1F2|,从而可得e的方程,即可求得双曲线的离心率.
解答:
解:∵PQ是经过F1且垂直于x轴的双曲线的弦,∠PF2Q=90°,
∴|PF1|=|F1F2|
∴
=2c
∴e2-2e-1=0
∴e=1±
∵e>1
∴e=1+
故选:B.
∴|PF1|=|F1F2|
∴
| b2 |
| a |
∴e2-2e-1=0
∴e=1±
| 2 |
∵e>1
∴e=1+
| 2 |
故选:B.
点评:本题考查双曲线的离心率,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
 如图,在正方体ABCD-A1B1C1D1中,E,F分别是A1D1,B1C1的中点,则与直线CF互为异面直线的是( )
如图,在正方体ABCD-A1B1C1D1中,E,F分别是A1D1,B1C1的中点,则与直线CF互为异面直线的是( )| A、CC1 |
| B、B1C1 |
| C、DE |
| D、AE |
已知等差数列{an}的公差为2,若a3是a1与a4的等比中项,则a2=( )
| A、-4 | B、-6 | C、-8 | D、-10 |
已知定义域为R的函数y=f(x)在[0,7]上只有1和3两个零点,且y=f(2-x)与y=(7+x)都是偶函数,则函数y=f(x)在[-2013,2013]上的零点个数为( )
| A、804 | B、805 |
| C、806 | D、807 |
有二种产品,合格率分别为0.90,0.95,各取一件进行检验,恰有一件不合格的概率为( )
| A、0.45 | B、0.14 |
| C、0.014 | D、0.045 |
有下列调查方式:
①学校为了解高一学生的数学学习情况,从每班抽2人进行座谈;
②一次数学竞赛中,某班有15人在100分以上,35人在90~100分,10人低于90分.现在从中抽取12人座谈了解情况;
③运动会中工作人员为参加400m比赛的6名同学公平安排跑道.
就这三个调查方式,最合适的抽样方法依次为( )
①学校为了解高一学生的数学学习情况,从每班抽2人进行座谈;
②一次数学竞赛中,某班有15人在100分以上,35人在90~100分,10人低于90分.现在从中抽取12人座谈了解情况;
③运动会中工作人员为参加400m比赛的6名同学公平安排跑道.
就这三个调查方式,最合适的抽样方法依次为( )
| A、分层抽样,系统抽样,简单随机抽样 |
| B、系统抽样,系统抽样,简单随机抽样 |
| C、分层抽样,简单随机抽样,简单随机抽样 |
| D、系统抽样,分层抽样,简单随机抽样 |
“x-2>0”是“x>1”的( )
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
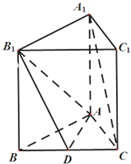 如图所示,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10,D是BC边的中点.
如图所示,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10,D是BC边的中点.