题目内容
16.在等差数列{an}中,a2+a7=-23,a3+a8=-29(1)求数列{an}的通项公式;
(2)设数列{an+bn}是首项为1,公比为2的等比数列,求{bn}的前n项和Sn.
分析 (1)依题意 a3+a8-(a2+a7)=2d=-6,从而d=-3.由此能求出数列{an}的通项公式.
(2)由数列{an+bn}是首项为1,公比为2的等比数列,求出${b_n}={2^{n-1}}-{a_n}$=3n-2+2n-1,再分组求和即可
解答 解:(1)设等差数列{an}的公差是d.
由已知(a3+a8)-(a2+a7)=2d=-6,
∴d=-3,
∴a2+a7=2a1+7d=-23m,
得 a1=-1,
∴数列{an}的通项公式为an=-3n+2
(2)由数列{an+bn}是首项为1,公比为2的等比数列,
∴${a_n}+{b_n}={2^{n-1}}$,
∴${b_n}={2^{n-1}}-{a_n}$=3n-2+2n-1,
∴Sn=[1+4+7+…+(3n-2)]+(1+2+22+…+2n-1)
=$\frac{{n({3n-1})}}{2}+{2^n}-1$,
=$\frac{{3{n^2}+n}}{2}$
点评 本题考查数列的通项公式和前n项和公式的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
2.已知向量$\overrightarrow{OA}$,$\overrightarrow{OB}$满足|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=2,$\overrightarrow{OA}$•$\overrightarrow{OB}$=2,若$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,且λ+μ=1(λ,μ∈R),则|$\overrightarrow{OC}$|的最小值为( )
| A. | 1 | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
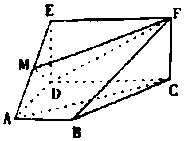 如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,AB=AD=DE=$\frac{1}{2}$CD,M是线段AE上的动点.
如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,AB=AD=DE=$\frac{1}{2}$CD,M是线段AE上的动点.