题目内容
6.设函数f(x)=x2-xlnx+2,若存在区间$[{a,b}]⊆[{\frac{1}{2},+∞})$,使f(x)在[a,b]上的值域为[k(a+2),k(b+2)],则k的取值范围为(1,$\frac{9+2ln2}{10}$).分析 判断f(x)的单调性得出f(x)=k(x+2)在[$\frac{1}{2}$,+∞)上有两解,作出函数图象,利用导数的意义求出k的范围.
解答 解:f′(x)=2x-lnx+1,f″(x)=2-$\frac{1}{x}$,
∴当x≥$\frac{1}{2}$时,f″(x)≥0,
∴f′(x)在[$\frac{1}{2}$,+∞)上单调递增,
∴f′(x)≥f′($\frac{1}{2}$)=2-ln$\frac{1}{2}$>0,
∴f(x)在[$\frac{1}{2}$,+∞)上单调递增,
∵[a,b]⊆[$\frac{1}{2}$,+∞),
∴f(x)在[a,b]上单调递增,
∵f(x)在[a,b]上的值域为[k(a+2),k(b+2)],
∴$\left\{\begin{array}{l}{f(a)=k(a+2)}\\{f(b)=k(b+2)}\end{array}\right.$,∴方程f(x)=k(x+2)在[$\frac{1}{2}$.+∞)上有两解a,b.
作出y=f(x)与直线y=k(x+2)的函数图象,则两图象有两交点.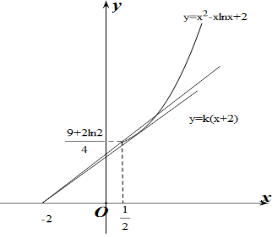
若直线y=k(x+2)过点($\frac{1}{2}$,$\frac{9}{4}+\frac{1}{2}ln2$),则k=$\frac{9+2ln2}{10}$,
若直线y=k(x+2)与y=f(x)的图象相切,设切点为(x0,y0),
则$\left\{\begin{array}{l}{{y}_{0}=k({x}_{0}+2)}\\{{y}_{0}={{x}_{0}}^{2}-{x}_{0}ln{x}_{0}+2}\\{2{x}_{0}-ln{x}_{0}+1=k}\end{array}\right.$,解得k=1.
∴1<k<$\frac{9+2ln2}{10}$.
故答案为:(1,$\frac{9+2ln2}{10}$).
点评 本题考查了函数的单调性,导数的几何意义,零点个数与函数图象的关系,属于中档题.

| A. | a=-8,b=-10 | B. | a=-4,b=-9 | C. | a=-1,b=9 | D. | a=-1,b=2 |
| 房型 | 特大套 | 大套 | 经济适用房 |
| 舒适 | 100 | 150 | x |
| 标准 | 300 | y | 600 |
(1)求x,y的值;
(2)在年终促销活动中,奖给了某优秀销售公司2套舒适型和3套标准型“经济适用型”套房,该销售公司又从中随机抽取了2套作为奖品回馈消费者.求至少有一套是舒适型套房的概率;
(3)今从“大套”类套房中抽取6套,进行各项指标综合评价,并打分如下:9.0 9.2 9.5 8.8 9.6 9.7
现从上面6个分值中随机的一个一个地不放回抽取,规定抽到数9.6或9.7,抽取工作即停止.记在抽取到数9.6或9.7所进行抽取的次数为ξ,求ξ的分布列及数学期望.

| A. | m>7? | B. | m≥7? | C. | m>8? | D. | m>9? |
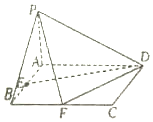 已知四棱锥P-ABCD底面ABCD是矩形,PA⊥平面ABCD,AD=4,AB=2,E,F分别是线段AB,BC的中点.
已知四棱锥P-ABCD底面ABCD是矩形,PA⊥平面ABCD,AD=4,AB=2,E,F分别是线段AB,BC的中点.