题目内容
11．展开式${（{{x^2}-\frac{2}{x^3}}）^5}$中的常数项为40．分析 根据二项展开式的通项公式，令x的指数等于0，求出r的值，即可求出展开式中的常数项．
解答 解：展开式${（{{x^2}-\frac{2}{x^3}}）^5}$的通项公式为
Tr+1=${C}_{5}^{r}$•（x2）5-r•${（-\frac{2}{{x}^{3}}）}^{r}$=（-2）r•${C}_{5}^{r}$•x10-5r，
令10-5r=0，解得r=2；
∴展开式中的常数项为
T3=（-2）2•${C}_{5}^{2}$=40．
故答案为：40．
点评 本题考查了二项展开式的通项公式应用问题，是基础题．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
1．某房屋开发公司根据市场调查，计划在2017年开发的楼盘中设计“特大套”、“大套”、“经济适用房”三类商品房，每类房型中均有舒适和标准两种型号．某年产量如表：
若按分层抽样的方法在这一年生产的套房中抽取50套进行检测，则必须抽取“特大套”套房10套，“大套”15套．
（1）求x，y的值；
（2）在年终促销活动中，奖给了某优秀销售公司2套舒适型和3套标准型“经济适用型”套房，该销售公司又从中随机抽取了2套作为奖品回馈消费者．求至少有一套是舒适型套房的概率；
（3）今从“大套”类套房中抽取6套，进行各项指标综合评价，并打分如下：9.0 9.2 9.5 8.8 9.6 9.7
现从上面6个分值中随机的一个一个地不放回抽取，规定抽到数9.6或9.7，抽取工作即停止．记在抽取到数9.6或9.7所进行抽取的次数为ξ，求ξ的分布列及数学期望．
| 房型 | 特大套 | 大套 | 经济适用房 |
| 舒适 | 100 | 150 | x |
| 标准 | 300 | y | 600 |
（1）求x，y的值；
（2）在年终促销活动中，奖给了某优秀销售公司2套舒适型和3套标准型“经济适用型”套房，该销售公司又从中随机抽取了2套作为奖品回馈消费者．求至少有一套是舒适型套房的概率；
（3）今从“大套”类套房中抽取6套，进行各项指标综合评价，并打分如下：9.0 9.2 9.5 8.8 9.6 9.7
现从上面6个分值中随机的一个一个地不放回抽取，规定抽到数9.6或9.7，抽取工作即停止．记在抽取到数9.6或9.7所进行抽取的次数为ξ，求ξ的分布列及数学期望．
2．若复数z满足z（1+i）=1-2i，其中i为虚数单位，则复数z对应的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
1．
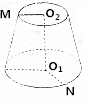如图，圆台的高为4，上、下底面半径分别为3、5，M、N分别在上、下底面圆周上，且＜$\overrightarrow{{O}_{2}M}$，$\overrightarrow{{O}_{1}N}$＞=120°，则|$\overrightarrow{MN}$|等于（ ）
如图，圆台的高为4，上、下底面半径分别为3、5，M、N分别在上、下底面圆周上，且＜$\overrightarrow{{O}_{2}M}$，$\overrightarrow{{O}_{1}N}$＞=120°，则|$\overrightarrow{MN}$|等于（ ）| A． | $\sqrt{65}$ | B． | 5$\sqrt{2}$ | C． | $\sqrt{35}$ | D． | 5 |