题目内容
正方体ABCD-A1B1C1D1的棱长为a,点M在A1C上,且AM=
MC1,N为BB1的中点,则MN的长为 .
| 1 |
| 2 |
考点:点、线、面间的距离计算
专题:空间向量及应用
分析:如图所示.建立空间直角坐标系,利用向量的坐标与模的计算公式即可得出.
解答:
解:如图所示,
N(a,a,
a),C1(0,a,a),A(a,0,0).
∵AM=
MC1,
∴
=
,
∴
=
+
=(a,0,0)+
(-a,a,a)
=(
a,
a,
a).
∴
=
-
=(
a,
a,
a),
∴|
|=
=
a.
故答案为:
a.

N(a,a,
| 1 |
| 2 |
∵AM=
| 1 |
| 2 |
∴
| AM |
| 1 |
| 3 |
| AC1 |
∴
| DM |
| DA |
| 1 |
| 3 |
| AC1 |
=(a,0,0)+
| 1 |
| 3 |
=(
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴
| MN |
| DN |
| DM |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 6 |
∴|
| MN |
|
| ||
| 6 |
故答案为:
| ||
| 6 |
点评:本题考查了向量的坐标与模的计算公式,属于基础题.

练习册系列答案
相关题目
将一张边长为6cm的纸片按如图1所示的阴影部分截去四个全等的等腰三角形,将剩余下部分沿虚线折叠并拼成一个有底的正四棱锥(底面是正方形,顶点在底面的射影为正方形的中心)模型,如图2放置,若正四棱锥的正视图是正三角形(如图3),则正四棱锥的体积是( )
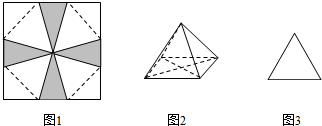

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
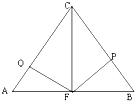 如图,CF是△ABC边AB上的高,FP⊥BC,FQ⊥AC.
如图,CF是△ABC边AB上的高,FP⊥BC,FQ⊥AC.