题目内容
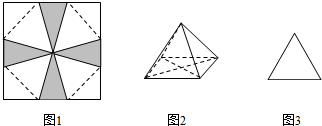
将一张边长为6cm的纸片按如图1所示的阴影部分截去四个全等的等腰三角形,将剩余下部分沿虚线折叠并拼成一个有底的正四棱锥(底面是正方形,顶点在底面的射影为正方形的中心)模型,如图2放置,若正四棱锥的正视图是正三角形(如图3),则正四棱锥的体积是( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:根据图形正四棱锥的正视图是正三角形,正视图的底面边长为a,高为
a,正四棱锥的斜高为a,运用图1得出;
×6=a+
,a=2
,计算计算出a,代入公式即可.
| ||
| 2 |
| ||
| 2 |
| a |
| 2 |
| 2 |
解答:
解:

∵正四棱锥的正视图是正三角形,正视图的底面边长为a,高为
a,
∴正四棱锥的斜高为a,
∵图1得出:∵将一张边长为6cm的纸片按如图1所示的阴影部分截去四个全等的等腰三角形
∴
×6=a+
,a=2
,
∴正四棱锥的体积是
×a2×
a=
,
故选:A

∵正四棱锥的正视图是正三角形,正视图的底面边长为a,高为
| ||
| 2 |
∴正四棱锥的斜高为a,
∵图1得出:∵将一张边长为6cm的纸片按如图1所示的阴影部分截去四个全等的等腰三角形
∴
| ||
| 2 |
| a |
| 2 |
| 2 |
∴正四棱锥的体积是
| 1 |
| 3 |
| ||
| 2 |
8
| ||
| 3 |
故选:A
点评:本题综合考查了空间几何体的性质,展开图与立体图的结合,需要很好的空间思维能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知复合命题p∧(¬q)是真命题,则下列命题中也是真命题的是( )
| A、(¬p)∨q |
| B、p∨q |
| C、p∧q |
| D、(¬p)∧(¬q) |
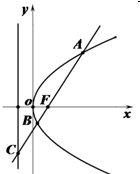 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=3|BF|,且|AF|=6,则此抛物线的方程为
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=3|BF|,且|AF|=6,则此抛物线的方程为