题目内容
若函数y=f(x)在x=x0处可导,则
= .
| lim |
| △x→0 |
| f(x0-2△x)-f(x0) |
| △x |
考点:极限及其运算
专题:导数的综合应用
分析:利用导数的定义即可得出.
解答:
解:∵函数y=f(x)在x=x0处可导,
则
=-2×
=-2f′(x0).
故答案为:-2f′(x0).
则
| lim |
| △x→0 |
| f(x0-2△x)-f(x0) |
| △x |
| lim |
| △x→0 |
| f(x0-2△x)-f(x0) |
| -2△x |
故答案为:-2f′(x0).
点评:本题考查了导数的定义,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
以原点O为中心,焦点在x轴上的双曲线C,有一条渐近线的倾斜角为60°,点F是该双曲线的右焦点.位于第一象限内的点M在双曲线C上,且点N是线段MF的中点.若|
|=|
|+1,则双曲线C的方程为( )
| ON |
| NF |
A、x2-
| ||||
B、x2-
| ||||
C、
| ||||
| D、3x2-y2=1 |
已知命题p:?x∈R,x2+2ax+2-a=0为真命题,则实数a的取值范围是( )
| A、a≥1或a≤-2 |
| B、a≤-2或1≤a≤2 |
| C、a≥1 |
| D、-2≤a≤1 |
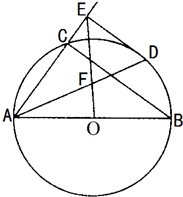 如图所示,⊙O的直径为AB,AD平分∠BAC,AD交⊙O于点D,BC∥DE,且DE交AC的延长线于点E,OE交AD于点F.
如图所示,⊙O的直径为AB,AD平分∠BAC,AD交⊙O于点D,BC∥DE,且DE交AC的延长线于点E,OE交AD于点F.