题目内容
8.已知双曲线的标准方程为$\frac{y^2}{2}-\frac{x^2}{4}$=1,则双曲线的渐近线方程为( )| A. | y=±2x | B. | $y=±\sqrt{2}x$ | C. | $y=±\frac{1}{2}x$ | D. | $y=±\frac{{\sqrt{2}}}{2}x$ |
分析 由双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a,b>0)的渐近线方程为y=±$\frac{a}{b}$x,求得双曲线的a,b,即可得到所求渐近线方程.
解答 解:由双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a,b>0),
可得渐近线方程为y=±$\frac{a}{b}$x,
双曲线的标准方程为$\frac{y^2}{2}-\frac{x^2}{4}$=1的a=$\sqrt{2}$,b=2,
可得渐近线方程为y=±$\frac{\sqrt{2}}{2}$x.
故选:D.
点评 本题考查双曲线的渐近线方程的求法,注意运用双曲线的方程和渐近线方程的关系,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.若抛物线y2=2px(p>0)的焦点为F,点A(3,2)在抛物线开口内,点P为抛物线上一点,当△APF的周长最小时,△APF的面积为1,则|PF|=( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
3.命题“经过圆外一点与圆相切的直线至少有一条”的否定是( )
| A. | 经过圆外一点与圆相切的直线至多有两条 | |
| B. | 经过圆外一点与圆相切的直线有两条 | |
| C. | 经过圆外一点与圆相切的直线不存在 | |
| D. | 经过圆外一点与圆相切的直线至多有一条 |
20.下列叙述中正确的是( )
| A. | 若a,b,c∈R,则“ax2+bx+c≥0”的充分条件是“b2-4ac≤0” | |
| B. | 若a,b,c∈R,则“ab2>cb2”的充要条件是“a>c” | |
| C. | “直线a∥b”是“直线a⊥平面α,直线b⊥平面α”的必要条件 | |
| D. | b2=ac是a,b,c成等比数列的充要条件 |

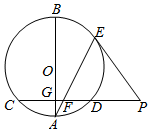 如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G,E是劣弧$\widehat{BD}$上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.
如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G,E是劣弧$\widehat{BD}$上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.