Question

4．如图，已知四边形ABCD是矩形，AB=1，BC=2，PD⊥平面ABCD，且PD=3，PB的中点E，求异面直线AE与PC所成角的大小．（用反三角表示）

Answer 1

分析 取BC的中点F，连接EF，AF、AE，推导出∠AEF（或者其补角）为异面直线AE与PC所成角，由此能求出异面直线AE与PC所成角的大小．

解答 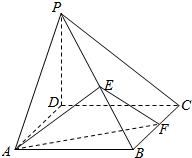解：取BC的中点F，连接EF，AF、AE，
∵E、F是中点，∴EF是△PBD的中位线，∴EF∥PB，
∴∠AEF（或者其补角）为异面直线AE与PC所成角，（3分）
∵四边形ABCD是矩形，AB=1，BC=2，PD⊥平面ABCD，
∴三垂线定理得PA⊥AB，
在Rt△PAB中，$PB=\sqrt{14，}AE=\frac{{\sqrt{14}}}{2}$（5分）
$PC=\sqrt{10}，EF=\frac{{\sqrt{10}}}{2}$（6分）
$AF=\sqrt{2}$，$AE=\frac{{\sqrt{14}}}{2}$，（7分）
由余弦定理，知$cos∠AEF=\frac{{A{E^2}+E{F^2}-A{F^2}}}{2AE•EF}$=$\frac{{{{（{\frac{{\sqrt{14}}}{2}}）}^2}+{{（{\frac{{\sqrt{10}}}{2}}）}^2}-{{（{\sqrt{2}}）}^2}}}{{2•\frac{{\sqrt{14}}}{2}•\frac{{\sqrt{10}}}{2}}}=\frac{{4\sqrt{35}}}{35}$，（10分）
∴$∠AEF=arccos\frac{{4\sqrt{35}}}{35}$（11分）
∴异面直线AE与PC所成角的大小$arccos\frac{{4\sqrt{35}}}{35}$．（12分）

点评 本题考查异面直线所成角的大小的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．