题目内容
10.下面有段演绎推理:“直线平行于平面,则该直线平行于平面内所有直线;
已知直线b?平面α,直线a?平面α,直线b∥平面α,
则直线b∥直线a”,则该推理中( )
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 该推理是正确的 |
分析 演绎推理的错误有三种可能,一种是大前提错误,第二种是小前提错误,第三种是逻辑结构错误,要判断推理过程的错误原因,可以对推理过程的大前提和小前提及推理的整个过程,细心分析,不难得到正确的答案.
解答 解:直线平行于平面,则直线可与平面内的直线平行、异面、异面垂直.
故大前提错误,结论错误.
故选:A,
点评 本题考查的知识点是演绎推理的基本方法及空间中线面关系,在使用三段论推理证明中,如果命题是错误的,则可能是“大前提”错误,也可能是“小前提”错误,也可能是逻辑错误.

练习册系列答案
相关题目
18.已知集合A={2,4,6},集合B={1},则A∪B等于( )
| A. | {1,2,4,6} | B. | {0,1,8,10} | C. | {0,8,10} | D. | ∅ |
5.log${\;}_{\frac{1}{2}}$|x-$\frac{π}{3}$|≥log${\;}_{\frac{1}{2}}$$\frac{π}{2}$的解集为( )
| A. | {x|-$\frac{π}{6}$≤x≤$\frac{5}{6}$π} | B. | {x|x≤-$\frac{π}{6}$,或x≥$\frac{5}{6}$π} | ||
| C. | {x|-$\frac{π}{6}$≤x≤$\frac{5}{6}$π且x≠$\frac{π}{3}$} | D. | {x|-$\frac{5π}{6}$≤x≤$\frac{5π}{6}$且x≠$\frac{π}{3}$} |
2.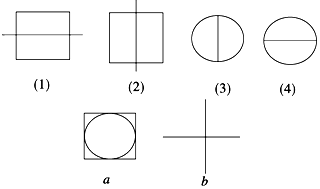 定义A*B,B*C,C*D,D*A的运算分别对应下面图中的(1),(2),(3),(4),则图中,a,b对应的运算是( )
定义A*B,B*C,C*D,D*A的运算分别对应下面图中的(1),(2),(3),(4),则图中,a,b对应的运算是( )
 定义A*B,B*C,C*D,D*A的运算分别对应下面图中的(1),(2),(3),(4),则图中,a,b对应的运算是( )
定义A*B,B*C,C*D,D*A的运算分别对应下面图中的(1),(2),(3),(4),则图中,a,b对应的运算是( )| A. | B*D,A*D | B. | B*D,A*C | C. | B*C,A*D | D. | C*D,A*D |
19.在△ABC中,BC:AB=2:$\sqrt{3}$,∠B=30°,则∠C=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
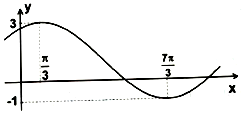 已知如图为f(x)=msin(ωx+φ)+n,m>0,ω>0的图象.
已知如图为f(x)=msin(ωx+φ)+n,m>0,ω>0的图象.