题目内容
计算:tan(-
)= .
| 26π |
| 3 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:直接利用诱导公式化简求值即可.
解答:
解:tan(-
)=-tan
=-tan(8π+
)=-tan
=tan
=
.
故答案为:
.
| 26π |
| 3 |
| 26π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| 3 |
故答案为:
| 3 |
点评:本题考查诱导公式的应用,三角函数的化简求值,基本知识的考查.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
已知全集U={0,1,2,3,4}且∁UA={0,2},则集合A的非空真子集共有( )
| A、5个 | B、6个 | C、7个 | D、8个 |
设A、B为椭圆
+
=1上任意两点,O为坐标原点,则“OA⊥OB”是“O到直线AB的距离为
”的( )
| x2 |
| 16 |
| y2 |
| 9 |
| 12 |
| 5 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
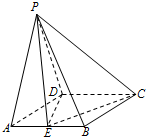 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PA=PD=3,PD⊥CD.E为AB中点.
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PA=PD=3,PD⊥CD.E为AB中点.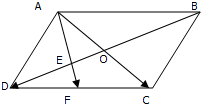 如图所示,已知?ABCD,E是OD的中点,
如图所示,已知?ABCD,E是OD的中点, 如图所示,在直三棱柱ABC-A1B1C1中,底面是等腰三角形,∠ACB=90°,侧棱AA1=2,CA=2,D是CC1的中点,试问在线段A1B上是否存在一点E(不与端点重合),使得点A1到平面AED的距离为
如图所示,在直三棱柱ABC-A1B1C1中,底面是等腰三角形,∠ACB=90°,侧棱AA1=2,CA=2,D是CC1的中点,试问在线段A1B上是否存在一点E(不与端点重合),使得点A1到平面AED的距离为