题目内容
等比数列{an}的各项均为正数，且a2a18=
，则log3a1+log3a3+log3a5+…+log3a19=（ ）
| 1 |
| 3 |
| A、5 | ||
| B、-5 | ||
C、
| ||
D、
|
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：根据等比数列的性质：中a2a18=
=
，再由对数运算法则求解．
| a | 2 10 |
| 1 |
| 3 |
解答：
解：等比数列中a2a18=
=
，所以log3a1+log3a3+…+log3a19=log3(a1a3…a19)=log3a1010=log3(
)5=-5
故选：B．
| a | 2 10 |
| 1 |
| 3 |
| 1 |
| 3 |
故选：B．
点评：等比数列{an}中，若m+n=p+q则aman=apaq，在对数运算中logab+logac=loga（bc）．
练习册系列答案
名校课堂系列答案
相关题目
曲线y=sinx与x轴在区间[0，2π]上所围成阴影部分的面积为（ ）
| A、-4 | B、-2 | C、2 | D、4 |
函数f（x）=
，则f（1）=（ ）
| 1 |
| 1-x+x2 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
已知点(
，2)在幂函数f（x）=xα（α＞0）的图象上，则f（x）的表达式是（ ）
| 2 |
| A、f（x）=x2 | ||
| B、f（x）=x-2 | ||
C、f（x）=x
| ||
D、f（x）=x-
|
设P={x|x≤8}，a=
，则下列关系中，正确的是（ ）
| 61 |
| A、a⊆P |
| B、a∉P |
| C、{a}∈P |
| D、{a}是P的真子集 |
已知某四棱锥的正视图和侧视图如图所示，则该四棱锥的俯视图为（ ）
A、 |
B、 |
C、 |
D、 |
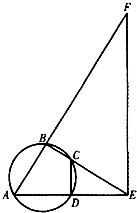如图，A、B、C、D四点共圆，BC和AD的延长线交于点E，点F在AB的延长线上．