题目内容
已知||x-2|-|x+1||≤2,求x的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:由题意可得可得-2≤|x-2|-|x+1|≤2,即
.利用绝对值的意义分别求得①、②的解集,再取交集,即得所求.
|
解答:
解:由已知||x-2|-|x+1||≤2,可得-2≤|x-2|-|x+1|≤2,即
.
由于|x-2|-|x+1|表示数轴上的x对应点到2对应点的距离减去它到-1对应点的距离,
而1.5对应点到2对应点的距离减去它到-1对应点的距离正好等于-2,故①的解集为{x|x≤1.5}.
而-0.5对应点到2对应点的距离减去它到-1对应点的距离正好等于2,故②的解集为{x|x≥-0.5}.
故不等式组的解集为{x|-0.5≤x≤1.5},
即原不等式的解集为{x|-0.5≤x≤1.5}.
|
由于|x-2|-|x+1|表示数轴上的x对应点到2对应点的距离减去它到-1对应点的距离,
而1.5对应点到2对应点的距离减去它到-1对应点的距离正好等于-2,故①的解集为{x|x≤1.5}.
而-0.5对应点到2对应点的距离减去它到-1对应点的距离正好等于2,故②的解集为{x|x≥-0.5}.
故不等式组的解集为{x|-0.5≤x≤1.5},
即原不等式的解集为{x|-0.5≤x≤1.5}.
点评:本题主要考查绝对值的意义,绝对值不等式的解法,关键是去掉绝对值,化为与之等价的不等式组来解,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
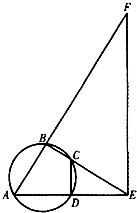 如图,A、B、C、D四点共圆,BC和AD的延长线交于点E,点F在AB的延长线上.
如图,A、B、C、D四点共圆,BC和AD的延长线交于点E,点F在AB的延长线上. 如图,五面体中,四边形ABCD是矩形,DA⊥平面ABEF,且DA=1,AB∥EF,AB=
如图,五面体中,四边形ABCD是矩形,DA⊥平面ABEF,且DA=1,AB∥EF,AB=