题目内容
如图, 是以
是以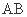 为直径的半圆上异于点
为直径的半圆上异于点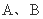 的点,矩形
的点,矩形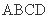 所在的平面垂直于该半圆所在平面,且
所在的平面垂直于该半圆所在平面,且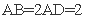 .
.
(Ⅰ)求证: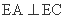 ;
;
(Ⅱ)设平面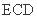 与半圆弧的另一个交点为
与半圆弧的另一个交点为
①. 求证: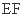 //
//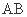 ;
;
②. 若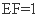 ,求多面体
,求多面体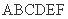 的体积V.
的体积V.
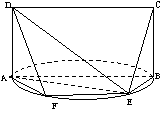
解:(Ⅰ)∵E是半圆上异于A、B的点,∴AE⊥EB,
又∵矩形平面ABCD⊥平面ABE,且CB⊥AB,
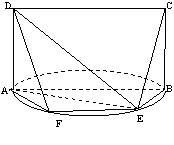 由面面垂直性质定理得:CB⊥平面ABE,∴平面CBE⊥平面ABE,
由面面垂直性质定理得:CB⊥平面ABE,∴平面CBE⊥平面ABE,
且二面交线为EB,由面面垂直性质定理得:
AE⊥平面ABE,又EC在平面ABE 内,故得:EA⊥EC…………4分
内,故得:EA⊥EC…………4分
(Ⅱ) ①由CD//AB,得CD//平面ABE,又∵平面CDE∩平面ABE于直线EF,∴根据线面平行的性质定理得:
CD//EF,CD//AB,故EF//AB …………7分
②分别取AB、EF的中点为O、M,连接OM,则在直角三角形OME中, ,
, 因为矩形
因为矩形 所在的平面垂直于该半圆所在平面,
所在的平面垂直于该半圆所在平面,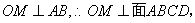 即OM为M到面ABCD之距,又
即OM为M到面ABCD之距,又
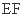 //
//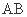 ,
, E到到面ABCD之距也为
E到到面ABCD之距也为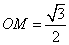 , …………9分
, …………9分
则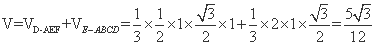 …………12分
…………12分

练习册系列答案
相关题目
为了解高三学生综合素质测评情况,对2000名高三学生的测评结果进行了统计,其中优秀、良好、合格三个等级的男、女学生人数如下表:
| 优秀 | 良好 | 合格 | |
| 男生人数 |
| 380 | 373 |
| 女生人数 |
| 370 | 377 |
(Ⅰ)若按优秀、良好、合格三个等级分层,在这2000份综合素质测评结果中随机抽取80份进行比较分析,应抽取综合素质测评结果是优秀等级的多少份?
(Ⅱ)若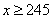 ,
,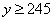 ,求优秀等级的学生中男生人数比女生人数多的概率.
,求优秀等级的学生中男生人数比女生人数多的概率.
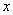
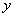
 组
组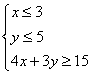 所表示的平面区域为D.若圆C落在区
所表示的平面区域为D.若圆C落在区 的焦点
的焦点 恰好是曲线
恰好是曲线  的右焦点,且曲线
的右焦点,且曲线 与曲线
与曲线 交点连线过点
交点连线过点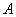 .
.
 .
.
 .
.
 .
.
 的不等式
的不等式 无解,则实数
无解,则实数 的取值范围为 .
的取值范围为 .  ,直线m⊂平面
,直线m⊂平面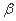 ,则“
,则“ D.既不充分又不必要条件
D.既不充分又不必要条件 和直线
和直线 ,抛物线
,抛物线 上一动点
上一动点 到直线
到直线 和直线
和直线 的距离之和的最小值( )
的距离之和的最小值( ) D.
D.
 ,则输出
,则输出 的值是
的值是
 :
: ,
, ;命题
;命题 :
: ,
, .
. 是假命题 B.
是假命题 B. 是真命题 D.
是真命题 D. 是真命题
是真命题