题目内容
17.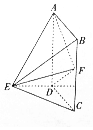 在多面体ABCDE中,ABCD是矩形,平面ABCD⊥平面CDE,CD⊥DE,2DE=2DC=BC,F是棱BC的中点.
在多面体ABCDE中,ABCD是矩形,平面ABCD⊥平面CDE,CD⊥DE,2DE=2DC=BC,F是棱BC的中点.(1)证明:AF⊥EF;
(2)已知CD=1,求点B到平面AEF的距离.
分析 (1)连结DF,AF.证明ED⊥AF,AF⊥DF,得到AF⊥面DEF,即可得到AF⊥EF.
(2)利用VB-AEF=VE-ABF 求解.
解答 解:(1)证明: 连结DF,AF.
连结DF,AF.
平面ABCD⊥平面CDE,平面ABCD∩平面CDE=CD,CD⊥DE,∴DE⊥面ABCD.
∴ED⊥AF,
在矩形ABCD中,AB=DC=CF=FB,∴∠CFD=∠BFA=90°.即AF⊥DF,
∴AF⊥面DEF,又因为EF?面EFD,∴AF⊥EF.
(2)设点B到平面AEF的距离为h,且2DE=2DC=BC=2
∵VB-AEF=VE-ABF,∴$\frac{1}{3}×{s}_{△AEF}×h=\frac{1}{3}×{s}_{ABF}×ED$.,EF=$\sqrt{E{D}^{2}+C{D}^{2}+C{F}^{2}}=\sqrt{3}$
∵${s}_{△AEF}=\frac{1}{2}×AE×EF=\frac{1}{2}×\sqrt{2}×\sqrt{3}=\frac{\sqrt{6}}{2}$,${s}_{△ABF}=\frac{1}{2}×AB×BF=\frac{1}{2}$,
解得h=$\frac{\sqrt{6}}{6}$,即B到平面AEF的距离为$\frac{\sqrt{6}}{6}$
点评 本题考查了空间线线垂直的判定,等体积法求点面距离,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.已知函数f(x)=-x3+ax2-x-2在(-∞,+∞)上是单调函数,则实数a的取值范围是( )
| A. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | B. | (-$\sqrt{3}$,$\sqrt{3}$) | C. | (-∞,-$\sqrt{3}$]∪[$\sqrt{3}$,+∞) | D. | [-$\sqrt{3}$,$\sqrt{3}$] |
6.设直线x-y-a=0与圆x2+y2=4相交于A,B两点,O为坐标原点,若△AOB为等边三角形,则实数a的值为( )
| A. | $±\sqrt{3}$ | B. | $±\sqrt{6}$ | C. | ±3 | D. | ±9 |
5.设函数$f(x)={log_{\frac{1}{2}}}(a{x^2}+2x-1)$,$g(x)=\frac{{2+2sin(2x+\frac{π}{6})}}{{sinx+\sqrt{3}cosx}}$,若不论x2取何值,f(x1)>g(x2)对任意${x_1}∈[\frac{7}{10},\frac{3}{2}]$总是恒成立,则a的取值范围为( )
| A. | $(-∞,-\frac{7}{10})$ | B. | $(-∞,-\frac{4}{5})$ | C. | $(-\frac{63}{80},+∞)$ | D. | $(-\frac{40}{49},-\frac{4}{5})$ |
12.若函数f(x)满足f(2x-1)=x+1,则f(3)等于( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
6.已知函数$f(x)=\left\{\begin{array}{l}({a-1})x+4-2a,x<1\\ 1+{log_2}x,x≥1\end{array}\right.$,若f(x)的值域为R,则实数a的取值范围是( )
| A. | (1,2] | B. | (-∞,2] | C. | (0,2] | D. | [2,+∞) |
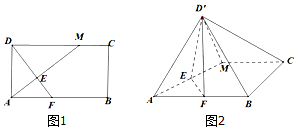 如图,在矩形ABCD中,AB=2BC,点M在边CD上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C,得四棱锥D′-ABCM.
如图,在矩形ABCD中,AB=2BC,点M在边CD上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C,得四棱锥D′-ABCM.