题目内容
14.设数列{an}的前n项和为Sn.已知a1=a,(a≠3)an+1=Sn+3n,n∈N*.(Ⅰ)设bn=Sn-3n,求数列{bn}的通项公式;
(Ⅱ)若an+1≥an,n∈N*,求a的取值范围.(文科求{an}的通项公式)
分析 (Ⅰ)由题意可知${b_n}={S_n}-{3^n}$,${b_{n+1}}={S_{n+1}}-{3^{n+1}}$,${b_{n+1}}+{3^{n+1}}=2({b_n}+{3^n})+{3^n}$,bn+1=2bn,则{bn}是首项是a-3,公比为2的等比数列,即可求得数列{bn}的通项公式;
(Ⅱ)由(Ⅰ)可知:求得数列{an}的通项公式,由指数函数的单调性,即可求得a的取值范围.
解答 解:(Ⅰ)由an+1=Sn+1-Sn,${a_{n+1}}={S_n}+{3^n}$
则${S_{n+1}}=2{S_n}+{3^n}$,${b_n}={S_n}-{3^n}$,${b_{n+1}}={S_{n+1}}-{3^{n+1}}$,
∴${S_n}={b_n}+{3^n}$,${S_{n+1}}={b_{n+1}}+{3^{n+1}}$,
∴${b_{n+1}}+{3^{n+1}}=2({b_n}+{3^n})+{3^n}$,
∴bn+1=2bn,a≠3,
∴b1=S1-3=a-3≠0,
∴{bn}是首项是a-3,公比为2的等比数列,
∴数列{bn}的通项公式${b_n}=({a-3})•{2^{n-1}}$;
(Ⅱ)∵${b_n}={S_n}-{3^n}$,∴${S_n}={3^n}+({a-3})•{2^{n-1}}$,Sn-1=3n-1+(a-3)•2n-2,
n≥2时,an=Sn-Sn-1=2×3n-1+(a-3)2n-2,
a1=a≠$\frac{1}{2}$(a-3)+2,
an=$\left\{\begin{array}{l}{a}&{n=1}\\{(a-3)•{2}^{n-2}+2×{3}^{n-1}}&{n≥2}\end{array}\right.$,
a2=a+3>a1,
${a_{n+1}}≥{a_n}?2×{3^n}+({a-3}){2^{n-1}}≥2×{3^{n-1}}+({a-3}){2^{n-2}}?8×{({\frac{3}{2}})^{n-1}}+a-3≥0$,
∵n≥2时,$8×{({\frac{3}{2}})^{n-1}}≥12$,
由指数函数的性质可知8×($\frac{3}{2}$)n-1,在R上单调递增,
则a-3≥-12,解得:a≥-9,
a的取值范围[-9,+∞).
点评 本题考查等比数列通项公式,考查数列通项公式的求法,指数函数的性质,考查函数单调性的应用,考查计算能力,属于中档题.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $(-∞,-\frac{7}{10})$ | B. | $(-∞,-\frac{4}{5})$ | C. | $(-\frac{63}{80},+∞)$ | D. | $(-\frac{40}{49},-\frac{4}{5})$ |
| A. | 3 | B. | 4 | C. | 5 | D. | 与P的位置有关 |
| A. | (1,2] | B. | (-∞,2] | C. | (0,2] | D. | [2,+∞) |
(Ⅰ)根据已知条件完成下面的2×2列联表:据此材料,是否有95%的把握认为投票结果与性别有关?
| 支持希拉里 | 支持特朗普 | 合计 | |
| 男员工 | |||
| 女员工 | |||
| 合计 |
附:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
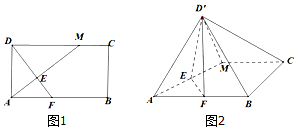 如图,在矩形ABCD中,AB=2BC,点M在边CD上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C,得四棱锥D′-ABCM.
如图,在矩形ABCD中,AB=2BC,点M在边CD上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C,得四棱锥D′-ABCM.