题目内容
不等式|2x-4|+1≤ax的解集非空,则a的取值范围是 .
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:作出f(x)=|2x-4|+1与y=ax的图象,要使不等式|2x-4|+1≤ax的解集非空,利用图象,数形结合,分析即可求得a的取值范围.
解答:
解:作出f(x)=|2x-4|+1与y=ax的图象,如下图:
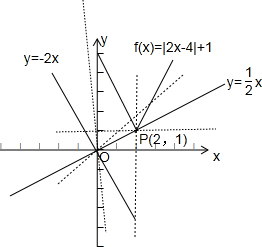
|2x-4|+1≤ax的解集非空的几何意义是:y=ax的图象与y=|2x-4|+1的图象相切或y=ax的图象在y=|2x-4|+1的图象的上方,
图中的y=
x和y=-2x表示不等式f(x)≤ax的解集非空的临界情况,
由图可知,a≥
或a<-2时,y=ax与V型区域上方必有交点,不等式|2x-4|+1≤ax的解集非空,
故答案为:a≥
或a<-2.

|2x-4|+1≤ax的解集非空的几何意义是:y=ax的图象与y=|2x-4|+1的图象相切或y=ax的图象在y=|2x-4|+1的图象的上方,
图中的y=
| 1 |
| 2 |
由图可知,a≥
| 1 |
| 2 |
故答案为:a≥
| 1 |
| 2 |
点评:本题考查绝对值不等式的解法,作图是关键,考查数形结合思想与分析、解决问题的能力,属于中档题.

练习册系列答案
相关题目
函数y=log5-x(2x-3)的定义域为( )
A、(
| ||
B、(
| ||
| C、(4,5) | ||
D、(
|
 已知f(x)=
已知f(x)=