题目内容
20.若点M是以椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1的短轴为直径的圆在第一象限内的一点,过点M作该圆的切线交椭圆E于P,Q两点,椭圆E的右焦点为F2,则△PF2Q的周长是6.分析 方法一、设直线PQ的方程为y=kx+m(k<0,m>0),联立椭圆方程,设P(x1,y1),Q(x2,y2),运用韦达定理和弦长公式,结合直线和圆相切的条件:d=r,化简整理,可得周长;
方法二、设P(x1,y1),Q(x2,y2),运用椭圆的焦半径公式和勾股定理,化简整理即可得到所求周长.
解答 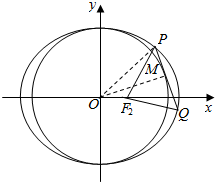 解:根据题意作出图形如图所示,
解:根据题意作出图形如图所示,
方法一、设直线PQ的方程为y=kx+m(k<0,m>0),
由$\left\{\begin{array}{l}y=kx+m\\ \frac{x^2}{9}+\frac{y^2}{8}=1\end{array}\right.$得(8+9k2)x2+18kmx+9m2-72=0,
有△=(18km)2-4(8+9k2)(9m2-72)=288(9k2-m2+8)>0,
设P(x1,y1),Q(x2,y2),则${x_1}+{x_2}=\frac{-18km}{{8+9{k^2}}}$,${x_1}{x_2}=\frac{{9{m^2}-72}}{{8+9{k^2}}}$,
∴$|{PQ}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|$
=$\sqrt{1+{k^2}}\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}$=$\sqrt{1+{k^2}}\sqrt{{{(\frac{-18km}{{8+9{k^2}}})}^2}-4×\frac{{9{m^2}-72}}{{8+9{k^2}}}}$
=$\sqrt{1+{k^2}}\sqrt{\frac{{4×9×8(9{k^2}-{m^2}+8)}}{{{{(8+9{k^2})}^2}}}}$.
∵直线PQ与圆x2+y2=8相切,
∴$\frac{m}{{\sqrt{1+{k^2}}}}=2\sqrt{2}$,即$m=\sqrt{8(1+{k^2})}$,
∴$|{PQ}|=-\frac{6km}{{8+9{k^2}}}$,
∵$|{P{F_2}}|=\sqrt{{{({x_1}-2)}^2}+y_1^2}$=$\sqrt{{{({x_1}-1)}^2}+8(1-\frac{x_1^2}{9})}$=$\sqrt{{{(\frac{x_1}{3}-3)}^2}}$,0<x1<3,
∴$|{P{F_2}}|=3-\frac{x_1}{3}$,同理$|{Q{F_2}}|=3-\frac{x_2}{3}$,
∴|PF2|+|QF2|+|PQ|=6-$\frac{{x}_{1}+{x}_{2}}{3}$-$\frac{6km}{8+9{k}^{2}}$=$6+\frac{6km}{{8+9{k^2}}}-\frac{6km}{{8+9{k^2}}}=6$,
因此,△PF2Q的周长是定值6.
方法二:设P(x1,y1),Q(x2,y2),
则$\frac{{{x}_{1}}^{2}}{9}$+$\frac{{{y}_{1}}^{2}}{8}$=1,|PF2|=$\sqrt{({x}_{1}-1)^{2}+{{y}_{1}}^{2}}$=$\sqrt{{{({x_1}-1)}^2}+8(1-\frac{x_1^2}{9})}$=$\sqrt{(\frac{{x}_{1}}{3}-3)^{2}}$,0<x1<3,
∴$|{P{F_2}}|=3-\frac{x_1}{3}$,又M是圆O的切点,连接OP,OM,
∴$|{PM}|=\sqrt{{{|{OP}|}^2}-{{|{OM}|}^2}}$=$\sqrt{x_1^2+y_1^2-8}$$\sqrt{x_1^2+8(1-\frac{x_1^2}{9})-8}$=$\frac{1}{3}{x_1}$,
∴$|{P{F_2}}|+|{PM}|=3-\frac{1}{3}{x_1}+\frac{1}{3}{x_1}=3$,
同理|QF2|+|QM|=3,
∴|PF2|+|QF2|+|PQ|=3+3=6,
因此,△PF2Q的周长是定值6.
故答案为:6.
点评 本题考查椭圆的定义、方程和性质,考查直线和圆相切的条件:d=r,考查运算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案
| A. |  | B. |  | C. |  | D. |  |
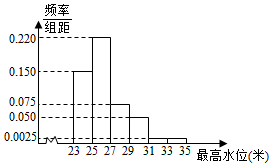 根据某水文观测点的历史统计数据,得到某河流每年最高水位X(单位:米)的频率分布直方图如图:
根据某水文观测点的历史统计数据,得到某河流每年最高水位X(单位:米)的频率分布直方图如图: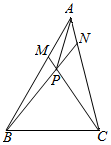 如图所示,在三角形ABC中,AM:AB=1:3,AN:AC=1:4,BN与CM相交于P,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{AP}$.
如图所示,在三角形ABC中,AM:AB=1:3,AN:AC=1:4,BN与CM相交于P,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{AP}$.