题目内容
11．在等比数列{an}中，公比q≠1，且a1+a2，a3+a4，a5+a6成等差数列，若a1+a2+a3=1，则a12+a22+…+a102=（ ）| A． | 1 | B． | 10 | C． | 32 | D． | 100 |
分析 由题意列关于等比数列的首项和公比的方程组，求解方程组得答案．
解答 解：在等比数列{an}中，公比q≠1，
由a1+a2，a3+a4，a5+a6成等差数列，且a1+a2+a3=1，
得$\left\{\begin{array}{l}{2（{a}_{3}+{a}_{4}）={a}_{1}+{a}_{2}+{a}_{5}+{a}_{6}}\\{{a}_{1}+{a}_{2}+{a}_{3}=1}\end{array}\right.$，即：
$\left\{\begin{array}{l}{2{a}_{1}（{q}^{2}+{q}^{3}）={a}_{1}（1+q+{q}^{4}+{q}^{5}）}\\{{a}_{1}（1+q+{q}^{2}）=1}\end{array}\right.$，解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{q=-1}\end{array}\right.$．
∴数列{${{a}_{n}}^{2}$}是常数列1，1，1，…，
则a12+a22+…+a102=10．
故选：B．
点评 本题考查等比数列的通项公式，考查方程组的解法，是基础题．
练习册系列答案
相关题目
1．
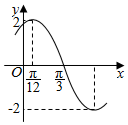已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，若将f（x）的图象上所有点向右平移$\frac{π}{12}$个单位得到函数g（x）的图象，则函数g（x）的单调增区间为（ ）
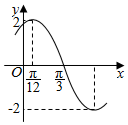已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，若将f（x）的图象上所有点向右平移$\frac{π}{12}$个单位得到函数g（x）的图象，则函数g（x）的单调增区间为（ ）| A． | $[kπ-\frac{π}{3}，kπ+\frac{π}{6}]$，k∈Z | B． | $[kπ+\frac{π}{6}，kπ+\frac{2π}{3}]$，k∈Z | ||
| C． | $[kπ-\frac{π}{12}，kπ+\frac{π}{12}]$，k∈Z | D． | $[kπ-\frac{7π}{12}，kπ-\frac{π}{12}]$，k∈Z |
2．已知f（x）是定义域为R的偶函数，且当x≥0时，f（x）=（$\frac{1}{2}$）x，则不等式f（x）＞$\frac{1}{2}$的解集为（ ）
| A． | （-$\frac{1}{4}$，$\frac{1}{4}$） | B． | （-$\frac{1}{2}$，$\frac{1}{2}$） | C． | （-2，2） | D． | （-1，1） |
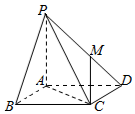如图，在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，PA⊥底面ABCD，PA=AB，点M在棱PD上，PB∥平面ACM．
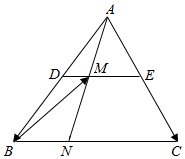如图，在△ABC中，D，E分别是AB，AC的中点，DM=$\frac{1}{3}$DE，若$\overrightarrow{AB}$=a，$\overrightarrow{AC}$=b．