题目内容
10．若函数f（x）=ln（x+$\sqrt{a+{x}^{2}}$）为奇函数，则a=1．分析 由f（x）为奇函数便可得到$ln（-x+\sqrt{a+{x}^{2}}）=-ln（x+\sqrt{a+{x}^{2}}）$，进行分子有理化和对数的运算便可得到$ln（-x+\sqrt{a+{x}^{2}}）=ln\frac{a}{x+\sqrt{a+{x}^{2}}}$=$lna-ln（x+\sqrt{a+{x}^{2}}）$，从而便可得出lna=0，这便得到a=1．
解答 解：f（x）为奇函数；
∴f（-x）=-f（x）；
即$ln（-x+\sqrt{a+{x}^{2}}）=ln\frac{a}{x+\sqrt{a+{x}^{2}}}$=$lna-ln（x+\sqrt{a+{x}^{2}}）=-ln（x+\sqrt{a+{x}^{2}}）$；
∴lna=0；
∴a=1．
故答案为：1．
点评 考查奇函数的定义，以及分子有理化和对数的运算性质．
练习册系列答案
相关题目
20．在1，2，3，4四个数中随机地抽取一个数记为a，再在剩余的三个数中随机地抽取一个数记为b，则“$\frac{a}{b}$不是整数”的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{4}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
1．
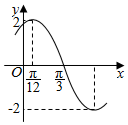已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，若将f（x）的图象上所有点向右平移$\frac{π}{12}$个单位得到函数g（x）的图象，则函数g（x）的单调增区间为（ ）
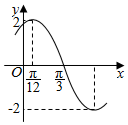已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，若将f（x）的图象上所有点向右平移$\frac{π}{12}$个单位得到函数g（x）的图象，则函数g（x）的单调增区间为（ ）| A． | $[kπ-\frac{π}{3}，kπ+\frac{π}{6}]$，k∈Z | B． | $[kπ+\frac{π}{6}，kπ+\frac{2π}{3}]$，k∈Z | ||
| C． | $[kπ-\frac{π}{12}，kπ+\frac{π}{12}]$，k∈Z | D． | $[kπ-\frac{7π}{12}，kπ-\frac{π}{12}]$，k∈Z |
18．已知复数z=1+i，则z4=（ ）
| A． | -4i | B． | 4i | C． | -4 | D． | 4 |
5．某商场举行优惠促销活动，顾客仅可以从以下两种优惠方案中选择一种，
方案一：每满200元减50元：
方案二：每满200元可抽奖一次．具体规则是依次从装有3个红球、1个白球的甲箱，装有2个红球、2个白球的乙箱，以及装有1个红球、3个白球的丙箱中各随机摸出1个球，所得结果和享受的优惠如下表：（注：所有小球仅颜色有区别）
（Ⅰ）若两个顾客都选择方案二，各抽奖一次，求至少一个人获得半价优惠的概率；
（Ⅱ）若某顾客购物金额为320元，用所学概率知识比较哪一种方案更划算？
方案一：每满200元减50元：
方案二：每满200元可抽奖一次．具体规则是依次从装有3个红球、1个白球的甲箱，装有2个红球、2个白球的乙箱，以及装有1个红球、3个白球的丙箱中各随机摸出1个球，所得结果和享受的优惠如下表：（注：所有小球仅颜色有区别）
| 红球个数 | 3 | 2 | 1 | 0 |
| 实际付款 | 半价 | 7折 | 8折 | 原价 |
（Ⅱ）若某顾客购物金额为320元，用所学概率知识比较哪一种方案更划算？
2．已知f（x）是定义域为R的偶函数，且当x≥0时，f（x）=（$\frac{1}{2}$）x，则不等式f（x）＞$\frac{1}{2}$的解集为（ ）
| A． | （-$\frac{1}{4}$，$\frac{1}{4}$） | B． | （-$\frac{1}{2}$，$\frac{1}{2}$） | C． | （-2，2） | D． | （-1，1） |