题目内容
10．
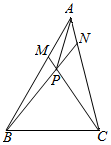如图所示，在三角形ABC中，AM：AB=1：3，AN：AC=1：4，BN与CM相交于P，若$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，试用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{AP}$．
分析 根据条件可得$\overrightarrow{AN}=\frac{1}{4}\overrightarrow{AC}，\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$，从而由B，P，N三点共线便可得到$\overrightarrow{AP}=（1-λ）\overrightarrow{AB}+\frac{λ}{4}\overrightarrow{AC}$，而同理由C，P，M三点共线可得到$\overrightarrow{AP}=（1-μ）\overrightarrow{AC}+\frac{μ}{3}\overrightarrow{AB}$，这样根据平面向量基本定理便可得到$\left\{\begin{array}{l}{1-λ=\frac{μ}{3}}\\{\frac{λ}{4}=1-μ}\end{array}\right.$，可以解出λ，这样即可用$\overrightarrow{a}，\overrightarrow{b}$表示出$\overrightarrow{AP}$．
解答 解：B，P，N三点共线；
∴$\overrightarrow{BP}=λ\overrightarrow{BN}$；
∴$\overrightarrow{AP}-\overrightarrow{AB}=λ（\overrightarrow{AN}-\overrightarrow{AB}）$；
∴$\overrightarrow{AP}=（1-λ）\overrightarrow{AB}+λ\overrightarrow{AN}$=$（1-λ）\overrightarrow{AB}+\frac{λ}{4}\overrightarrow{AC}$；
同理由C，P，M三点共线可得$\overrightarrow{AP}=（1-μ）\overrightarrow{AC}+\frac{μ}{3}\overrightarrow{AB}$；
∴由平面向量基本定理得$\left\{\begin{array}{l}{1-λ=\frac{μ}{3}}\\{\frac{λ}{4}=1-μ}\end{array}\right.$；
解得$λ=\frac{8}{11}$；
∴$\overrightarrow{AP}=\frac{3}{11}\overrightarrow{a}+\frac{2}{11}\overrightarrow{b}$．
点评 考查共线向量基本定理，向量减法、数乘的几何意义，以及向量的数乘运算，平面向量基本定理．
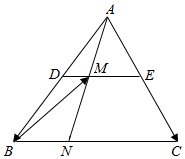如图，在△ABC中，D，E分别是AB，AC的中点，DM=$\frac{1}{3}$DE，若$\overrightarrow{AB}$=a，$\overrightarrow{AC}$=b．
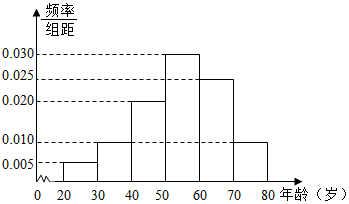广场舞是现代城市群众文化、娱乐发展的产物，其兼具文化性和社会性，是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区跳广场舞的人的年龄进行了凋查，随机抽取了40名广场舞者进行调查，将他们年龄分成6段：[20，30），[30，40），[40，50），[50，60），[60，70），[70，80]后得到如图所示的频率分布直方图．
| A． | f（sinA）＞f（cosA） | B． | f（cosA）＞f（sinA） | C． | f（cosA）＞f（sinB） | D． | f（sinA）＞f（cosB） |