题目内容

8．若不等式a2+b2≥2kab对任意a、b∈R都成立，则实数k的取值范围是[-1，1]．

分析 化简a2+b2-2kab=（a-kb）2+b2-k2b2，从而可得b2-k2b2≥0恒成立，从而解得．

解答 解：∵a2+b2-2kab=（a-kb）2+b2-k2b2，
∴对任意k，b，都存在a=kb；
∴不等式a2+b2≥2kab对任意a、b∈R都成立可化为：
b2-k2b2≥0恒成立，
即1-k2≥0成立，
故k∈[-1，1]，
故答案为：[-1，1]．

点评 本题考查了学生的化简运算能力及恒成立问题的应用．

练习册系列答案
相关题目
18．已知复数z=1+i，则z4=（　　）
A．-4iB．4iC．-4D．4
19．设椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率为$\frac{2}{3}\sqrt{2}$，且内切于圆x2+y2=9．
（1）求椭圆C的方程；
（2）过点Q（1，0）作直线l（不与x轴垂直）与该椭圆交于M、N两点，与y轴交于点R，若$\overrightarrow{RM}$=λ$\overrightarrow{MQ}$，$\overrightarrow{RN}$=$μ\overrightarrow{NQ}$，试判断λ+μ是否为定值，并说明理由．
16．设一四棱锥的体积为V，那么由各棱中点连线所组成的十面体的体积为$\frac{5V}{8}$．
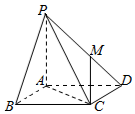3．如图，在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，PA⊥底面ABCD，PA=AB，点M在棱PD上，PB∥平面ACM．
（1）试确定点M的位置，并说明理由；
（2）求二面角M-AC-D的正切值．
13．给出下列命题：
①若$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|-|{\overrightarrow b}|$，则存在实数λ，使得$\overrightarrow b=λ\overrightarrow a$；
②$a={log_{\frac{1}{3}}}2，b={log_{\frac{1}{2}}}3，c={（{\frac{1}{3}}）^{0.5}}$大小关系是c＞a＞b；
③已知直线l1：ax+3y-1=0，l2：x+by+1=0，则l1⊥l2的充要条件是$\frac{a}{b}=-3$；
④已知a＞0，b＞0，函数y=2aex+b的图象过点（0，1），则$\frac{1}{a}+\frac{1}{b}$的最小值是$4\sqrt{2}$．其中正确命题的序号是①② （把你认为正确的序号都填上）．
20．若点M是以椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1的短轴为直径的圆在第一象限内的一点，过点M作该圆的切线交椭圆E于P，Q两点，椭圆E的右焦点为F2，则△PF2Q的周长是6．
17．已知{an}是等差数列，公差d不为零，且a3+a9=a10-a8，则a5=（　　）
A．-1B．0C．1D．2
18．已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率e=$\frac{\sqrt{6}}{3}$，F1、F2为其左、右焦点，M为椭圆E上一点，且△MF1F2面积的最大值为4$\sqrt{2}$．
（1）求椭圆E的标准方程；
（2）设直线l：y=x+m（m∈R）与椭圆E交于不同两点A、B，且|AB|=3$\sqrt{2}$，P为直线y=2上一点，满足|$\overrightarrow{PA}$|=|$\overrightarrow{PB}$|，求点P的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网