题目内容
 在三棱锥A-BCD中,AB=BC=4,AD=BD=CD=2
在三棱锥A-BCD中,AB=BC=4,AD=BD=CD=2| 2 |
| 2 |
(1)求证:CE∥平面ABD;
(2)如果二面角A-BD-C的大小为90°,求二面角C-AE-D的大小.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)由勾股定理得BD⊥CD,又CE⊥CD,从而CE∥BD,由此以证明CE∥平面ABD.
(2)以D为原点,DB、DC、DA分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角C-AE-D的大小.
(2)以D为原点,DB、DC、DA分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角C-AE-D的大小.
解答:
(1)证明:∵BD=CD=2
,BC=4,
∴BD2+CD2=BC2,∴BD⊥CD,
∵CE⊥CD,∴CE∥BD,
又CE不包含于平面ABD,BD?平面ABD,
∴CE∥平面ABD.
(2)解:∵二面角A-BD-C的大小为90°,AD⊥BD,
∴AD⊥平面BDC,又由(1)知BD⊥CD,
以D为原点,DB、DC、DA分别为x,y,z轴,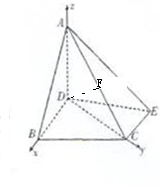
建立空间直角坐标系,又CE⊥CD,
∴CE⊥面ACD,又CE?平面ACE,
∴平面ACE⊥平面ACD,设AC中点为F,
连结DF,则DF⊥AC,且DF=2,DF⊥ACE,
由(1)知BD=CD=AD=2
,
B(
,2
,0),C(0,2
,0),
A(0,0,2
),F(0,
,
),
∴平面ACE的法向量
=(0,
,
),
同理,取ADE的法向量
=(2,1,0),
cos<
,
>=
=
.
∴二面角C-AE-D的大小为arccos
.
| 2 |
∴BD2+CD2=BC2,∴BD⊥CD,
∵CE⊥CD,∴CE∥BD,
又CE不包含于平面ABD,BD?平面ABD,
∴CE∥平面ABD.
(2)解:∵二面角A-BD-C的大小为90°,AD⊥BD,
∴AD⊥平面BDC,又由(1)知BD⊥CD,
以D为原点,DB、DC、DA分别为x,y,z轴,

建立空间直角坐标系,又CE⊥CD,
∴CE⊥面ACD,又CE?平面ACE,
∴平面ACE⊥平面ACD,设AC中点为F,
连结DF,则DF⊥AC,且DF=2,DF⊥ACE,
由(1)知BD=CD=AD=2
| 2 |
B(
| 2 |
| 2 |
| 2 |
A(0,0,2
| 2 |
| 2 |
| 2 |
∴平面ACE的法向量
| DF |
| 2 |
| 2 |
同理,取ADE的法向量
| n |
cos<
| n |
| DF |
| ||
2
|
| ||
| 10 |
∴二面角C-AE-D的大小为arccos
| ||
| 10 |
点评:本题考查直线与平面平行的证明,考查二面角的大小的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
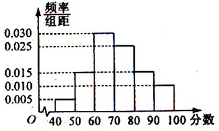 我校从高一年级学生中随机抽取部分学生,将他们的数学竞赛成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图.
我校从高一年级学生中随机抽取部分学生,将他们的数学竞赛成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图.