题目内容
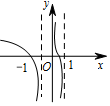
5.已知集合M={x|(x-3)(x+1)≤0},N={x|-2≤x≤2},则M∩N=( )| A. | [-1,2] | B. | [-2,-1] | C. | [-1,1] | D. | [1,2] |
分析 求出集合M中不等式的解集,确定出集合M,找出两解集的公共部分即可确定出两集合的交集
解答 解:由(x-3)(x+1)≥0,
解得:-1≤x≤3,
∴M={x|-1≤x≤3},
∵N={x|-2≤x≤2},
则M∩N={x|-1≤x≤2}=[-1,2]
故选A
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知某种商品的广告费支出x(单位;万元)与销售额y(单位:万元)之间有如下对应数据:
根据表中提供的全部数据,用最小二乘法得出y与x的线性回归方程为$\stackrel{∧}{y}$=6.5x+17.5,则表中m的值为( )
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | m | 70 |
| A. | 45 | B. | 50 | C. | 55 | D. | 60 |
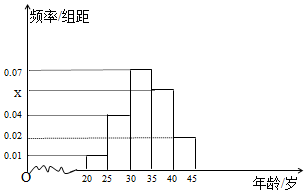 为响应国家“精准扶贫,产业扶贫”的战略,某市面向全市征召《扶贫政策》义务宣传志愿者,从年龄在[20,45]的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示.
为响应国家“精准扶贫,产业扶贫”的战略,某市面向全市征召《扶贫政策》义务宣传志愿者,从年龄在[20,45]的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示. 机器人AlphaGo(阿法狗)在下围棋时,令人称道算法策略是:每一手棋都能保证在接下来的十步后,局面依然是满意的.这种策略给了我们启示:每一步相对完美的决策,对最后的胜利都会产生积极的影响.下面的算法上算法是寻找“a1,a2,…,a10”中“比较大的数t”.现输入正整数“42,61,80,12,79,18,82,57,31,18”,从左到右依次为a1,a2,…,a10,其中最大的数记为T,则T-t=( )
机器人AlphaGo(阿法狗)在下围棋时,令人称道算法策略是:每一手棋都能保证在接下来的十步后,局面依然是满意的.这种策略给了我们启示:每一步相对完美的决策,对最后的胜利都会产生积极的影响.下面的算法上算法是寻找“a1,a2,…,a10”中“比较大的数t”.现输入正整数“42,61,80,12,79,18,82,57,31,18”,从左到右依次为a1,a2,…,a10,其中最大的数记为T,则T-t=( )