题目内容
4．
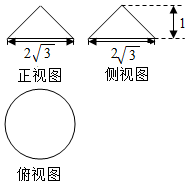某几何体的三视图如图所示，则该几何体的表面积为（ ）| A． | $\sqrt{3}π$ | B． | $2\sqrt{3}π$ | C． | $（{3+\sqrt{3}}）π$ | D． | $（{3+2\sqrt{3}}）π$ |
分析 判断三视图复原的几何体的形状，利用三视图的数据求解即可．
解答 解：三视图复原的几何体是圆锥，底面半径为：$\sqrt{3}$，高为：1，圆锥的母线长为：2，
圆锥的表面积为：$π×（\sqrt{3}）^{2}+π×\sqrt{3}×2$=（3+2$\sqrt{3}$）π．
故选：D．
点评 本题考查三视图与几何体的关系，几何体的表面积的求法，考查计算能力．
练习册系列答案
相关题目
19．设函数f（x）=cos（2x+$\frac{π}{4}$）+sin（2x+$\frac{π}{4}$），则（ ）
| A． | 函数f（x）在区间（$\frac{π}{2}，π$）内单调递增，其图象关于直线x=$\frac{π}{4}$对称 | |
| B． | 函数f（x）在区间（$\frac{π}{2}$，π）内单调递增，其图象关于直线x=$\frac{π}{2}$对称 | |
| C． | 函数f（x）在区间（$\frac{π}{2}$，π）内单调递减，其图象关于直线x=$\frac{π}{4}$对称 | |
| D． | 函数f（x）在区间（$\frac{π}{2}，π$）内单调递减，其图象关于直线x=$\frac{π}{2}$对称 |
9．已知m，n是不重合的两条直线，α，β是不重合的两个平面，则下列命题中错误的是（ ）
| A． | 若m⊥α，m⊥β，则α∥β | B． | 若m?α，m⊥β，则α⊥β | C． | 若m⊥α，n∥α，则m⊥n | D． | 若m⊥α，α⊥β，则m∥β |
16．已知双曲线的离心率为$\sqrt{3}$，一个焦点到一条渐近线的距离为2，则该双曲线的方程可以是（ ）
| A． | x2-$\frac{y^2}{4}$=1 | B． | x2-$\frac{y^2}{2}$=1 | C． | $\frac{y^2}{2}-\frac{x^2}{4}$=1 | D． | $\frac{y^2}{4}-\frac{x^2}{2}$=1 |
14．i（1-$\sqrt{3}$i）等于（ ）
| A． | $\sqrt{3}$-i | B． | $\sqrt{3}$+i | C． | -$\sqrt{3}$-i | D． | -$\sqrt{3}$+i |