题目内容
15.若复数z满足z2=$\frac{3}{4}$-i(i为虚数单位),则z的模为$\frac{\sqrt{5}}{2}$.分析 根据复数模的定义,直接求模即可.
解答 解:∵z2=$\frac{3}{4}$-i,
∴|z|2=|$\frac{3}{4}$-i|=$\sqrt{{(\frac{3}{4})}^{2}{+(-1)}^{2}}$=$\frac{5}{4}$,
∴z的模为|z|=$\frac{\sqrt{5}}{2}$.
故答案为:$\frac{\sqrt{5}}{2}$.
点评 本题主要考查了复数代数形式的乘除运算,以及复数模的计算问题,是基础题目.

练习册系列答案
相关题目
4.已知3x=2,3y=4,3z=8,则x,y,z为( )
| A. | 等差数列 | B. | 等比数列 | ||
| C. | 既是等差,又是等比数列 | D. | 都不是 |
4.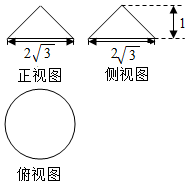 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )
 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )| A. | $\sqrt{3}π$ | B. | $2\sqrt{3}π$ | C. | $({3+\sqrt{3}})π$ | D. | $({3+2\sqrt{3}})π$ |
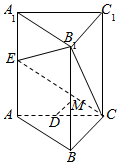 如图,直棱柱ABC-A1B1C1中,AB=AC=2,AA1=BC=2$\sqrt{3}$,E是AA1中点,D是AC的中点,M是BB1上一点,若DM∥平面B1CE,则$\frac{BM}{M{B}_{1}}$=3.
如图,直棱柱ABC-A1B1C1中,AB=AC=2,AA1=BC=2$\sqrt{3}$,E是AA1中点,D是AC的中点,M是BB1上一点,若DM∥平面B1CE,则$\frac{BM}{M{B}_{1}}$=3.